Solve f(x)=x³+4x² - 10 using the Newton-Raphson method for a root in [1, 2].
Solve f(x)=x³+4x² - 10 using the Newton-Raphson method for a root in [1, 2].
Introduction to Chemical Engineering Thermodynamics
8th Edition
ISBN:9781259696527
Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Publisher:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Chapter1: Introduction
Section: Chapter Questions
Problem 1.1P
Related questions
Question
![**Problem Statement:**
Solve \( f(x) = x^3 + 4x^2 - 10 \) using the Newton-Raphson method for a root in the interval \([1, 2]\).
**Explanation:**
To find the root of the given function within the specified interval using the Newton-Raphson method, follow these steps:
1. **Select an Initial Guess \( x_0 \):** Start with an initial guess within the interval, typically closer to where you anticipate the root might be.
2. **Calculate the Function's Derivative:** Compute the derivative \( f'(x) = 3x^2 + 8x \).
3. **Iterative Formula:** Use the formula
\[
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}
\]
to get successive approximations of the root.
4. **Convergence Check:** Repeat the iteration until the difference between successive approximations is within an acceptable tolerance or the function value \( f(x_n) \) is sufficiently close to zero.
5. **Result:** The value of \( x \) at which the iterations converge is the root.
This method is efficient and typically converges quickly if the initial guess is reasonable and the function behaves well.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F7447eb07-fceb-4d7b-a8f5-73349ee04b18%2F4e9111f6-7746-4692-844f-40d699c26e1a%2Fed41z2_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Solve \( f(x) = x^3 + 4x^2 - 10 \) using the Newton-Raphson method for a root in the interval \([1, 2]\).
**Explanation:**
To find the root of the given function within the specified interval using the Newton-Raphson method, follow these steps:
1. **Select an Initial Guess \( x_0 \):** Start with an initial guess within the interval, typically closer to where you anticipate the root might be.
2. **Calculate the Function's Derivative:** Compute the derivative \( f'(x) = 3x^2 + 8x \).
3. **Iterative Formula:** Use the formula
\[
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}
\]
to get successive approximations of the root.
4. **Convergence Check:** Repeat the iteration until the difference between successive approximations is within an acceptable tolerance or the function value \( f(x_n) \) is sufficiently close to zero.
5. **Result:** The value of \( x \) at which the iterations converge is the root.
This method is efficient and typically converges quickly if the initial guess is reasonable and the function behaves well.
Expert Solution
Step 1
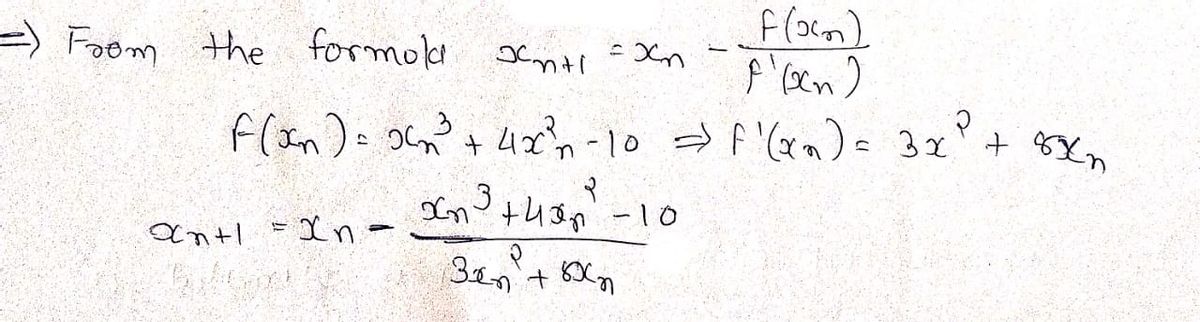
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Introduction to Chemical Engineering Thermodynami…
Chemical Engineering
ISBN:
9781259696527
Author:
J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Publisher:
McGraw-Hill Education

Elementary Principles of Chemical Processes, Bind…
Chemical Engineering
ISBN:
9781118431221
Author:
Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard
Publisher:
WILEY

Elements of Chemical Reaction Engineering (5th Ed…
Chemical Engineering
ISBN:
9780133887518
Author:
H. Scott Fogler
Publisher:
Prentice Hall

Introduction to Chemical Engineering Thermodynami…
Chemical Engineering
ISBN:
9781259696527
Author:
J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Publisher:
McGraw-Hill Education

Elementary Principles of Chemical Processes, Bind…
Chemical Engineering
ISBN:
9781118431221
Author:
Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard
Publisher:
WILEY

Elements of Chemical Reaction Engineering (5th Ed…
Chemical Engineering
ISBN:
9780133887518
Author:
H. Scott Fogler
Publisher:
Prentice Hall


Industrial Plastics: Theory and Applications
Chemical Engineering
ISBN:
9781285061238
Author:
Lokensgard, Erik
Publisher:
Delmar Cengage Learning

Unit Operations of Chemical Engineering
Chemical Engineering
ISBN:
9780072848236
Author:
Warren McCabe, Julian C. Smith, Peter Harriott
Publisher:
McGraw-Hill Companies, The