Determine the following: Reaction support at point B. a. 1350 lb (Upward Direction) b. 1380 lb(Downward Direction) c. 1400 lb (Upward Direction) d. 1420 lb (Downward Direction) Reaction support at point D. a. 600 lb (Upward Direction) b. 700 lb (Downward Direction) c. 800 lb (Upward Direction) d. 900 lb (Downward Direction) Centroid of the triangular load. a. 588 lb (Downward Direction) b. 598 lb (Upward Direction) c. 600 lb(Downward Direction) d. (Upward Direction)
Determine the following: Reaction support at point B. a. 1350 lb (Upward Direction) b. 1380 lb(Downward Direction) c. 1400 lb (Upward Direction) d. 1420 lb (Downward Direction) Reaction support at point D. a. 600 lb (Upward Direction) b. 700 lb (Downward Direction) c. 800 lb (Upward Direction) d. 900 lb (Downward Direction) Centroid of the triangular load. a. 588 lb (Downward Direction) b. 598 lb (Upward Direction) c. 600 lb(Downward Direction) d. (Upward Direction)
Elements Of Electromagnetics
7th Edition
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Sadiku, Matthew N. O.
ChapterMA: Math Assessment
Section: Chapter Questions
Problem 1.1MA
Related questions
Question
100%
Derive the shear force equation,bending moment equation for the beam shown. Neglect the weight of the beam.
Determine the following:
Reaction support at point B.
a. 1350 lb (Upward Direction)
b. 1380 lb(Downward Direction)
c. 1400 lb (Upward Direction)
d. 1420 lb (Downward Direction)
Reaction support at point D.
a. 600 lb (Upward Direction)
b. 700 lb (Downward Direction)
c. 800 lb (Upward Direction)
d. 900 lb (Downward Direction)
Centroid of the triangular load.
a. 588 lb (Downward Direction)
b. 598 lb (Upward Direction)
c. 600 lb(Downward Direction)
d. (Upward Direction)
Shear force equation for segment AB.
a.-16.65 psf X squared
b. 16.65 psf X squared
c. -16.75 psf X squared
d. 16.75 psf X squared
Bending moment equation for segment AB.
a.-5.40 psf X cube
b. 5.45 psf X cube
c. -5.55 psf X cube
d. 6.55 psf X cube
Shear force equation for segment BC.
a. 2000 lb - 200 lb/ft ( X)
b. 2100 lb - 300 lb/ft ( X)
c. 2150 lb - 300 lb/ft ( X)
d. 3000 lb - 200 lb/ft ( X)
Bending moment equation for segment BC.
a. 2000 lb(X) - 100 lb/ft (X squared) - 9600 lb-ft
b. 2100 lb(X) - 120 lb/ft (X squared) - 9700 lb-ft
c. 21500 lb(X) - 200 lb/ft (X squared) - 9800 lb-ft
d. 3000 lb(X) - 200 lb/ft (X squared) - 9850 lb-ft
The distance between point A and the shear force VAB=0
a. 6 feet
b. 8 feet
c. 10 feet
d. 12 feet
The degree of bending moment equations for segments AB and BC.
a. 1st degree and 2rd degree
b. 3rd degree and 2nd degree
c. 2nd degree and 3rd degree
d. None of the above.
Show complete solutions and diagram

Transcribed Image Text:A
6 ft-
200 lb/ft
B
CA
1200 lb. ft
★4 ft —— 4 ft -
D
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 3 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Solve for the Following
Shear force equation for segment AB.
a.-16.65 psf X squared
b. 16.65 psf X squared
c. -16.75 psf X squared
d. 16.75 psf X squared
Bending moment equation for segment AB.
a.-5.40 psf X cube
b. 5.45 psf X cube
c. -5.55 psf X cube
d. 6.55 psf X cube
Shear force equation for segment BC.
a. 2000 lb - 200 lb/ft ( X)
b. 2100 lb - 300 lb/ft ( X)
c. 2150 lb - 300 lb/ft ( X)
d. 3000 lb - 200 lb/ft ( X)
Bending moment equation for segment BC.
a. 2000 lb(X) - 100 lb/ft (X squared) - 9600 lb-ft
b. 2100 lb(X) - 120 lb/ft (X squared) - 9700 lb-ft
c. 21500 lb(X) - 200 lb/ft (X squared) - 9800 lb-ft
d. 3000 lb(X) - 200 lb/ft (X squared) - 9850 lb-ft
The distance between point A and the shear force VAB=0
a. 6 feet
b. 8 feet
c. 10 feet
d. 12 feet
The degree of bending moment equations for segments AB and BC.
a. 1st degree and 2rd degree
b. 3rd degree and 2nd degree
c. 2nd degree and 3rd degree
d. None of the above.
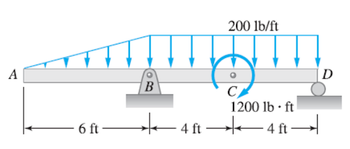
Transcribed Image Text:### Structural Analysis Education: Applied Forces and Moments on a Beam
#### Diagram Overview:
The diagram illustrates a beam subjected to various forces and moments. The beam is supported at three points: A, B, and D. The different sections and applied forces can be broken down as follows:
1. **Supports and Points:**
- Point A: Left end of the beam, not showing specific support type.
- Point B: Located 6 feet from Point A, where the beam is supported.
- Point C: Not a support point but marked indicating a moment and is positioned 4 feet to the right of Point B.
- Point D: Right end of the beam, located 4 feet to the right of Point C, also where the beam is supported.
2. **Distributed Load:**
- A linearly varying distributed load is applied to the beam from Point A to Point D.
- The distributed load increases from 0 lb/ft at Point A to 200 lb/ft at Point C. From Point B to Point D, the load is uniform at 200 lb/ft.
3. **Moment:**
- A counterclockwise moment of 1200 lb·ft is applied at Point C.
#### Detailed Explanation:
- **Beam Sections:**
- **Section AB (0 to 6 ft):** This section experiences a linearly increasing distributed load, starting from 0 lb/ft at A and increasing up to a maximum value of 200 lb/ft over the distance of 6 feet.
- **Section BC (6 ft to 10 ft):** This section has a constant distributed load of 200 lb/ft over the 4 feet leading up to Point C.
- **Section CD (10 ft to 14 ft):** This section continues with the constant distributed load of 200 lb/ft over the remaining 4 feet until the end of the beam at Point D.
- **Applied Moment at Point C:**
- At Point C, a counterclockwise moment of 1200 lb·ft is applied, represented in the diagram as a circular arrow centered around Point C.
#### Mathematical Formulations and Applications:
To analyze this beam, the following steps could be applied in a structural analysis context:
1. **Determine Support Reactions:**
- Calculate the reactions at supports B and D. Since Point A does not show a support type, assume it is not a
Solution
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education

Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education

Control Systems Engineering
Mechanical Engineering
ISBN:
9781118170519
Author:
Norman S. Nise
Publisher:
WILEY

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning

Engineering Mechanics: Statics
Mechanical Engineering
ISBN:
9781118807330
Author:
James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:
WILEY