со conjugates. CS.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Topic Video
Question
100%
Could you explain how to show 7.18 in detail? I also included lists of definitions and theorems in the book as a reference.

Transcribed Image Text:7.14. Let G be a finite group with normal subgroup N. Show that there are at least
as many conjugacy classes in G as in G/N.
7.18. Let G be a group and H the set of elements of G having only finitely many
conjugates. Show that H is a subgroup of G.
![Theorem 7.4. If G is any group, then conjugacy is an equivalence relation on the
elements of G.
Definition 7.3. Let G be a group and a e G. Then the conjugacy class of a is the
set Ca
= {g¬'ag : g e G}.
-1
Example 7.6. Note that Ca contains only a if and only if a e Z(G). (This happens
if and only if g¬'ag = a for all g e G.)
Example 7.7. Let k and n be positive integers with n > k. If G = S„ ando =
(1 2 3 ... k), then we see from Lemma 6.2 that C, is the set of all k-cycles in G.
It is important to know the size of a conjugacy class.
Lemma 7.1. Let G be a finite group and a E G. Then the number of elements in Ca
is the index of the centralizer, [G : C (a)].
Theorem 7.5 (Class Equation). Let G be a finite group, and let a1, ..
representatives of the conjugacy classes in G with more than one element. Then
ak be
..• .
|G| = |Z(G)|+[G: C(a1)]+ .+[G : C (ak)].
Corollary 7.1. Let G be a group of order p", for some prime p and positive integer
n. Then the centre of G is not trivial.
Corollary 7.2. Let G be a group of order p2, for some prime p. Then G is isomorphic
to either Z,2 or Z, × Zp.
Definition 7.4. Let G be a group and H a subgroup. We say that subgroups K and
L of G are H-conjugate if there exists an h e H such that h-'Kh = L. When
H = G, we simply say that K and L are conjugate.
Example 7.8. Let G be S5 and H = ((1 3)(2 5 4)). Take o = (1 3)(2 4 5) =
((1 3)(2 5 4))-l e H. Then we notice that
o(1 23 4)o = (1 3)(2 5 4)(1 2 3 4)(1 3)(2 4 5) = (1 2 3 5).
Therefore, for any integer i, o-(1 2 3 4)' o = (o¬1(1 2 3 4)0)' = (1 2 3 5)'. This
means that o-((1 2 3 4))o = ((1 2 3 5)). Thus, ((1 2 3 4)) and ((1 2 3 5)) are
H-conjugate (and, therefore, conjugate).
(o -1(1 2 3 4)o)
Theorem 7.6. Let G be a group and H a subgroup of G. Then H-conjugacy is an
equivalence relation on the set of all subgroups of G.
Theorem 7.7. Let G be a finite group and H a subgroup. Then for any subgroup K
of G, the number of H-conjugates of K in G is [H : NH(K)].](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F56be79ad-be6a-45f1-b897-58d23fd7e62d%2F7a83105a-42d1-4f6b-8025-d87bd0770d1b%2F6g9ni35_processed.png&w=3840&q=75)
Transcribed Image Text:Theorem 7.4. If G is any group, then conjugacy is an equivalence relation on the
elements of G.
Definition 7.3. Let G be a group and a e G. Then the conjugacy class of a is the
set Ca
= {g¬'ag : g e G}.
-1
Example 7.6. Note that Ca contains only a if and only if a e Z(G). (This happens
if and only if g¬'ag = a for all g e G.)
Example 7.7. Let k and n be positive integers with n > k. If G = S„ ando =
(1 2 3 ... k), then we see from Lemma 6.2 that C, is the set of all k-cycles in G.
It is important to know the size of a conjugacy class.
Lemma 7.1. Let G be a finite group and a E G. Then the number of elements in Ca
is the index of the centralizer, [G : C (a)].
Theorem 7.5 (Class Equation). Let G be a finite group, and let a1, ..
representatives of the conjugacy classes in G with more than one element. Then
ak be
..• .
|G| = |Z(G)|+[G: C(a1)]+ .+[G : C (ak)].
Corollary 7.1. Let G be a group of order p", for some prime p and positive integer
n. Then the centre of G is not trivial.
Corollary 7.2. Let G be a group of order p2, for some prime p. Then G is isomorphic
to either Z,2 or Z, × Zp.
Definition 7.4. Let G be a group and H a subgroup. We say that subgroups K and
L of G are H-conjugate if there exists an h e H such that h-'Kh = L. When
H = G, we simply say that K and L are conjugate.
Example 7.8. Let G be S5 and H = ((1 3)(2 5 4)). Take o = (1 3)(2 4 5) =
((1 3)(2 5 4))-l e H. Then we notice that
o(1 23 4)o = (1 3)(2 5 4)(1 2 3 4)(1 3)(2 4 5) = (1 2 3 5).
Therefore, for any integer i, o-(1 2 3 4)' o = (o¬1(1 2 3 4)0)' = (1 2 3 5)'. This
means that o-((1 2 3 4))o = ((1 2 3 5)). Thus, ((1 2 3 4)) and ((1 2 3 5)) are
H-conjugate (and, therefore, conjugate).
(o -1(1 2 3 4)o)
Theorem 7.6. Let G be a group and H a subgroup of G. Then H-conjugacy is an
equivalence relation on the set of all subgroups of G.
Theorem 7.7. Let G be a finite group and H a subgroup. Then for any subgroup K
of G, the number of H-conjugates of K in G is [H : NH(K)].
Expert Solution
Step 1
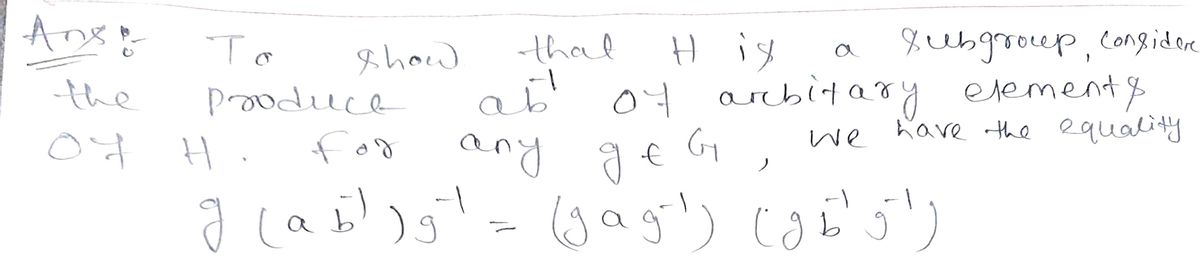
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

