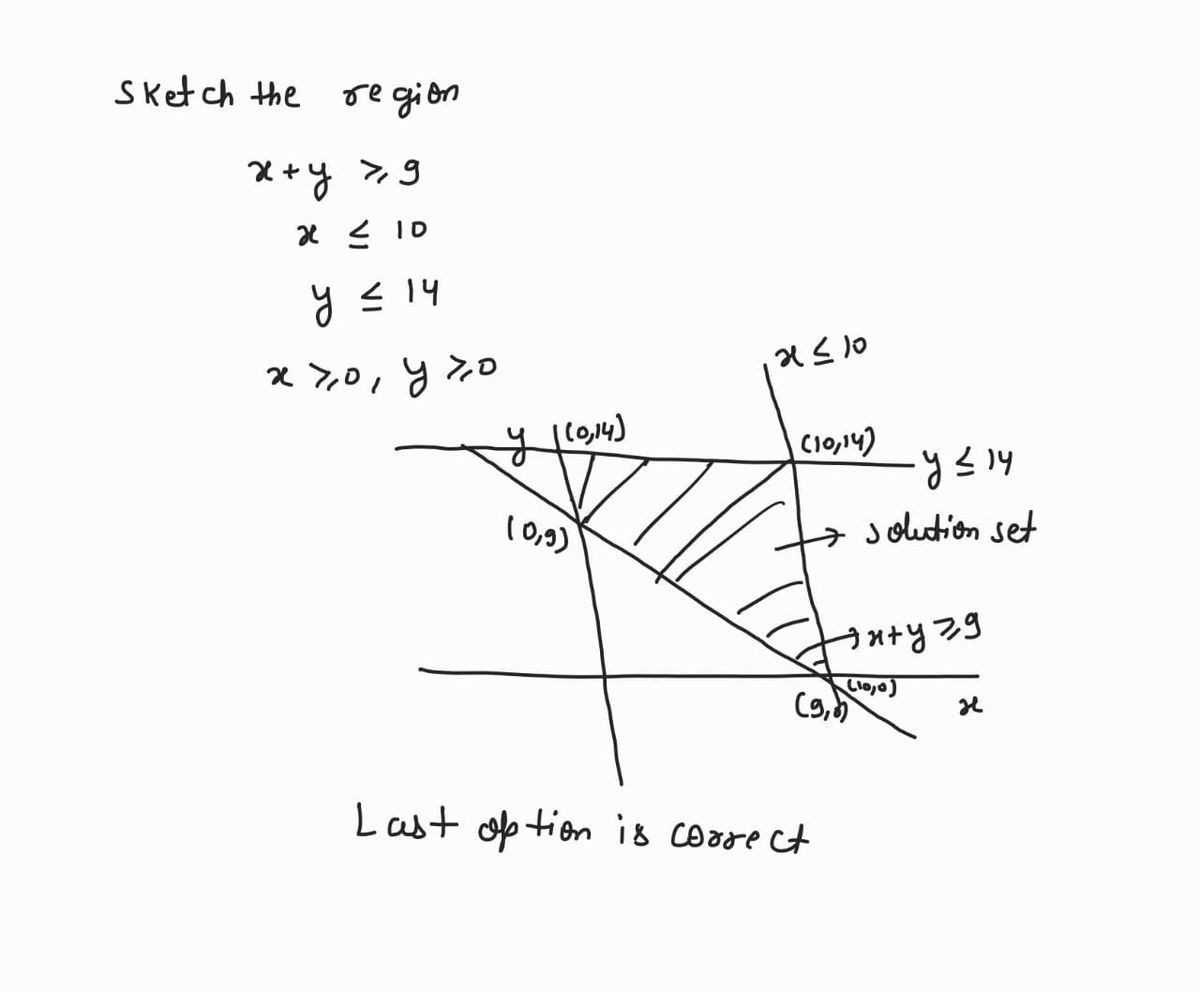
Sketch the region that corresponds to the given inequalities. (image attached of the question)x + y ≥ 9x ≤ 10 y ≤ 14x ≥ 0, y ≥ 0 Say whether the region is bounded or unbounded.The region is bounded.The region is unbounded. Find the coordinates of all corner points (if any). (Order your answers from smallest to largest x, then from smallest to largest y. If an answer does not exist, enter DNE.)(x, y) = (x, y) = (x, y) = (x, y) = (x, y) = The problem requires sketching the region that corresponds to a set of inequalities:1. \(x + y \geq 9\)2. \(x \leq 10\)3. \(y \leq 14\)4. \(x \geq 0\), \(y \geq 0\)There are four different graphs provided. Each graph is a coordinate plane with:- The x-axis ranging from \(-5\) to \(20\).- The y-axis ranging from \(-20\) to \(20\).- A highlighted blue solution set region.**Graph Analysis:**1. **First Graph:** - The solution set is shown in blue, primarily in the first quadrant. - Boundaries: - A vertical line at \(x = 10\) - A horizontal line at \(y = 14\) - A diagonal line from \((0,9)\) to \((9,0)\), representing \(x + y = 9\)2. **Second Graph:** - Similar to the first graph but different shading within the solution. - Boundaries: - Identical to the first graph.3. **Third Graph:** - Solution set is altered to a different section of the coordinate plane. - Boundaries: - Same constraints as the previous graphs.4. **Fourth Graph:** - Solution set moved again. - Boundaries remain unchanged; only shaded area representing the solution set moves.**Other Information:**There's a question at the bottom to determine if the region is bounded or unbounded. Additionally, there's a task to find the coordinates of all corner points in the region, in increasing order of \(x\) and \(y\), specifying that if an answer doesn't exist, enter "DNE."Each corner point can be found by solving the inequalities simultaneously to determine points of intersection:- **(\(x, y\)) =** - **(\(x, y\)) =** - **(\(x, y\)) =** - **(\(x, y\)) =** - **(\(x, y\)) =**

Answered: Image /qna-images/answer/a86db4e2-de40-4fcf-ad9a-1d3bf88385c5.jpg

Sketch the region that corresponds to the given inequalities. (image attached of the question) x + y ≥ 9 x ≤ 10 y ≤ 14 x ≥ 0, y ≥ 0 Say whether the region is bounded or unbounded. The region is bounded.The region is unbounded. Find the coordinates of all corner points (if any). (Order your answers from smallest to largest x, then from smallest to largest y. If an answer does not exist, enter DNE.)

Sketch the region that corresponds to the given inequalities. (image attached of the question) x + y ≥ 9 x ≤ 10 y ≤ 14 x ≥ 0, y ≥ 0 Say whether the region is bounded or unbounded. The region is bounded.The region is unbounded. Find the coordinates of all corner points (if any). (Order your answers from smallest to largest x, then from smallest to largest y. If an answer does not exist, enter DNE.)

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

Sketch the region defined by the inequalities - Choose the correct graph below. O A. Q -2≤rs4 and B. Л 1-750572 A O C. N O D. K
Graph the solution set. 2x - 2y <4 O No Solution ? Help -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 L 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 Clear All Delete Fill WebAssign. Graphing Tool Graph Layers After you add an object to the graph you can use Graph Layers to view and edit its properties.
............ .. Sketch the region that corresponds to the given inequalities. 4x + 3y < 4 4x - 3y 2 4 -y 2 2 y y y y 10 10 10 10- Solution Set Solution Set -10 -5 5 10 -10 -5 5 10 -10 -5 5 10 -10 -5 5 10 Solution Set -5 -5 Solution Set -5 -5 10 - 10 -10 -10- Say whether the region is bounded or unbounded. O The region is bounded. O The region is unbounded. Find the coordinates of all corner points (if any). (If an answer does not exist, enter DNE.) smaller x-value (х, у) 3 larger x-value (x, y) =
Please explain all subparts. I will really upvote
Which set of inequalities describes the shaded region in the following graph? 2.5 2 1.5 (0, 3) (0, 1) 0.5 (-3, 0) -3.5 (-1, 0) (1, 0) (3, 0) -2.5 -2 -1.5 -0.5 0 0.5 1.5 2 2.5 3.5 01≤≤3 and 1 ≤ y ≤3 Or>1 and 0 ≤0≤2 01≤r≤3 and 0 ≤0≤2 O-3≤ x ≤3 and -√√9-S None of the above -0.5 (0, -1) -1.5 -2 -2.5 (0,-3)
You have the class period to complete your exam during. You MUST SHOW WORK to receive credit! All work must be your own original work. No notes or books are allowed. Only an approved calculator may be used. No sharing of calculators allowed. Sprece, 1) Describe in words the region of R³ represented by 1 ≤ x² + y² + z² ≤5 the inequalities: X
B. Pick a point that is a solution and verify your solution region algebraically. Be sure to check each inequality and show your work below. Point: es. Substitute your-point into: y 2 |x - 3|- 6 C. Is (3, 0) a solution? D. Is (1, 3) a solution? E. Is (-2, 4) a solution? F. Is (0, -2) a solution?