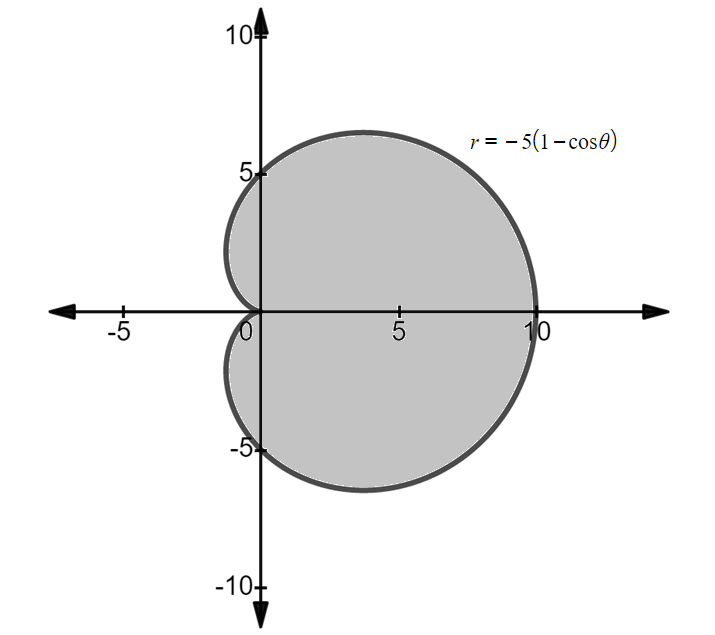
Sketch the region and use a double integral to find its area. The region bounded by the cardioid r= - 5(1 - cos 0)
Angles in Circles
Angles within a circle are feasible to create with the help of different properties of the circle such as radii, tangents, and chords. The radius is the distance from the center of the circle to the circumference of the circle. A tangent is a line made perpendicular to the radius through its endpoint placed on the circle as well as the line drawn at right angles to a tangent across the point of contact when the circle passes through the center of the circle. The chord is a line segment with its endpoints on the circle. A secant line or secant is the infinite extension of the chord.
Arcs in Circles
A circular arc is the arc of a circle formed by two distinct points. It is a section or segment of the circumference of a circle. A straight line passing through the center connecting the two distinct ends of the arc is termed a semi-circular arc.
Please help. Thank you.
![## Calculating the Area Bounded by a Cardioid
**Objective:**
To sketch the region and use a double integral to find its area.
### Problem Statement:
Determine the area of the region bounded by the cardioid defined by the polar equation:
\[ r = -5(1 - \cos \theta) \]
### Steps to Solve:
1. **Sketch the Cardioid:**
- Begin by plotting the polar equation \( r = -5(1 - \cos \theta) \). Note that this cardioid is reflected due to the negative sign in front of the function.
2. **Set Up the Double Integral:**
- The area \( A \) of a region in polar coordinates can be determined using the double integral:
\[
A = \frac{1}{2} \int_{\theta_1}^{\theta_2} r^2 \, d\theta
\]
- For this cardioid, determine \( \theta_1 \) and \( \theta_2 \), the limits of integration that will fully trace the curve.
3. **Evaluate the Integral:**
- Substitute the given equation into the integral:
\[
A = \frac{1}{2} \int_{\theta_1}^{\theta_2} [-5(1 - \cos \theta)]^2 \, d\theta
\]
- Solve the integral to find the exact area enclosed by the cardioid.
4. **Interpret the Result:**
- The resulting area will represent the space enclosed by the cardioid in the polar coordinate system.
By following these steps, you can accurately determine the area enclosed within this particular cardioid using double integrals in polar coordinates.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F8735dee1-ec31-4346-b70c-e4d10f64e04c%2F7f348b62-c483-4430-85e4-6a4f4976b730%2F5xekbqx.png&w=3840&q=75)
We have to find the area of the region bounded by the cardioid .
Using a graphing utility, sketch the polar curve and shade the region bounded by this cardioid as follows.
Step by step
Solved in 2 steps with 1 images









