Sketch the level curves of the function corresponding to each value of z. f(x, y) = √√√25 - x² - y²; z = 0, 1, 2, 3, 4 6 2 O -6 -4 -2 2 -2 O -6 y -4 -6- y 6 4 2 2 -4 -6- 2 4 6 6 X -6 DO -4 y 6 4 6 4 6 X y 6 2 O -6 -4 -2 2 -2 X
Sketch the level curves of the function corresponding to each value of z. f(x, y) = √√√25 - x² - y²; z = 0, 1, 2, 3, 4 6 2 O -6 -4 -2 2 -2 O -6 y -4 -6- y 6 4 2 2 -4 -6- 2 4 6 6 X -6 DO -4 y 6 4 6 4 6 X y 6 2 O -6 -4 -2 2 -2 X
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please help me with this question.
![### Level Curves of a Function
The function we are considering is:
\[ f(x, y) = \sqrt{25 - x^2 - y^2} \]
We need to sketch the level curves for the values \( z = 0, 1, 2, 3, 4 \).
#### Graph Explanation:
The image shows multiple graphs of concentric circles, each representing the level curves for different values of \( z \).
1. **Top Left Graph**:
- **z = 0 to 4**: The circles are at positions \( x = 0, y = 0 \).
- Radius increases with \( z \), from \( 0 \) up to nearly \( 5 \) for \( z=4 \).
2. **Top Middle Graph**:
- **z = 4**: Exhibits only a single large circle with a maximum radius.
3. **Top Right Graph**:
- **z = 3 to 4**: Series of increasingly larger circles.
- Supports visualizing how radius decreases as the value of \( z \) decreases.
4. **Bottom Graph**:
- Displays intermediate circles from **z = 2 to 4**.
- Highlights progression with decreasing radius as \( z \) reduces down to lower values.
#### Understanding Level Curves:
- Each circle represents points where the function \( f(x, y) \) attains the same value \( z \).
- The equations of the circles have the form \( x^2 + y^2 = r^2 \), where \( r = \sqrt{25 - z^2} \).
- As \( z \) increases from 0 to 4, the radius \( r \) decreases.
These graphs provide a visual representation of how the function behaves across a two-dimensional plane for different constant values. Understanding these level curves is crucial in multivariable calculus for visualizing potential fields, heat maps, and other applied mathematics scenarios.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F104f3f51-b974-4e41-a4df-f553c757aaae%2F191e97fe-6076-4e7c-9dd6-f4aa10169959%2Fydhamdj_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Level Curves of a Function
The function we are considering is:
\[ f(x, y) = \sqrt{25 - x^2 - y^2} \]
We need to sketch the level curves for the values \( z = 0, 1, 2, 3, 4 \).
#### Graph Explanation:
The image shows multiple graphs of concentric circles, each representing the level curves for different values of \( z \).
1. **Top Left Graph**:
- **z = 0 to 4**: The circles are at positions \( x = 0, y = 0 \).
- Radius increases with \( z \), from \( 0 \) up to nearly \( 5 \) for \( z=4 \).
2. **Top Middle Graph**:
- **z = 4**: Exhibits only a single large circle with a maximum radius.
3. **Top Right Graph**:
- **z = 3 to 4**: Series of increasingly larger circles.
- Supports visualizing how radius decreases as the value of \( z \) decreases.
4. **Bottom Graph**:
- Displays intermediate circles from **z = 2 to 4**.
- Highlights progression with decreasing radius as \( z \) reduces down to lower values.
#### Understanding Level Curves:
- Each circle represents points where the function \( f(x, y) \) attains the same value \( z \).
- The equations of the circles have the form \( x^2 + y^2 = r^2 \), where \( r = \sqrt{25 - z^2} \).
- As \( z \) increases from 0 to 4, the radius \( r \) decreases.
These graphs provide a visual representation of how the function behaves across a two-dimensional plane for different constant values. Understanding these level curves is crucial in multivariable calculus for visualizing potential fields, heat maps, and other applied mathematics scenarios.
Expert Solution
Step 1: Case z = 0
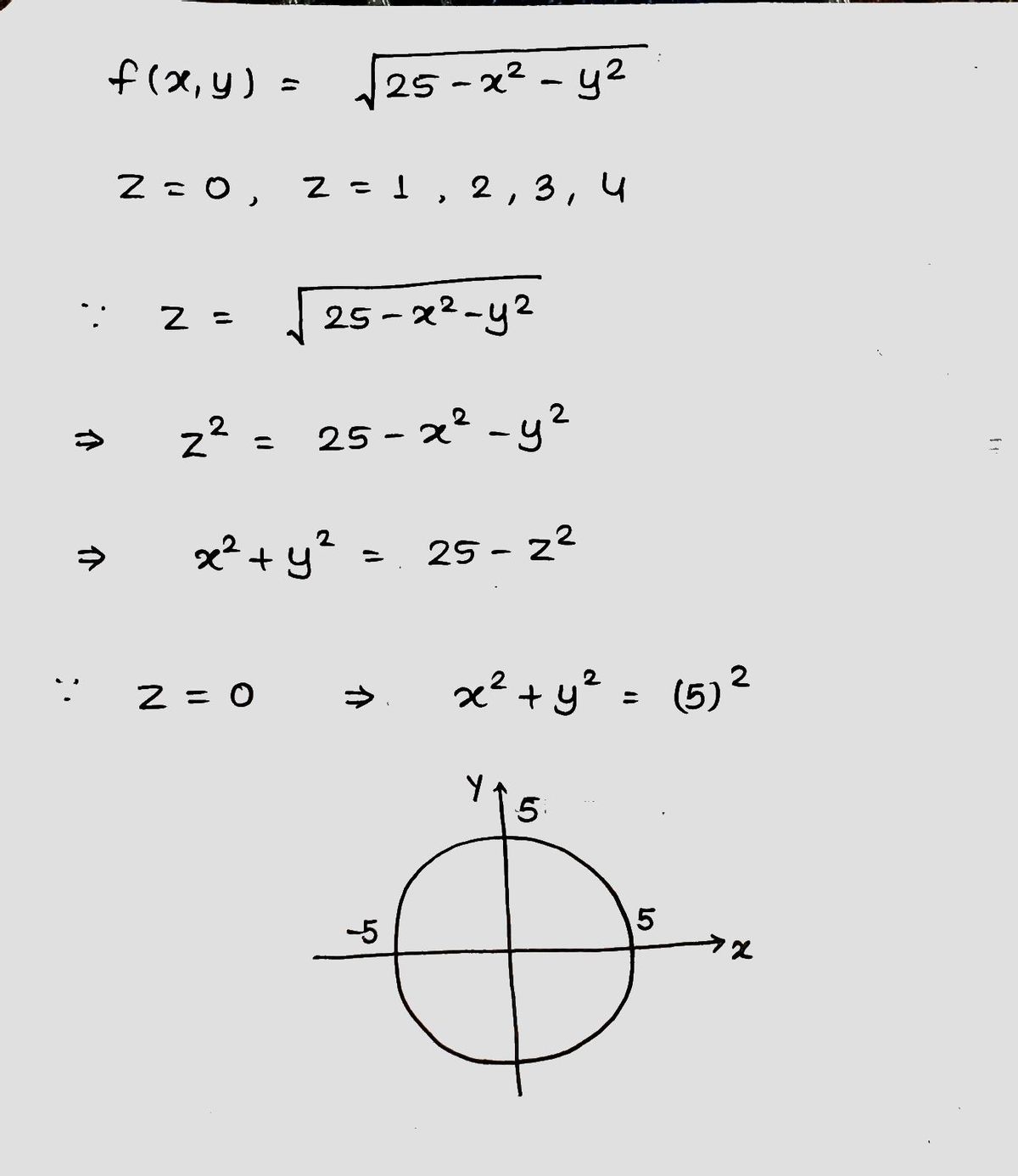
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

