Sketch the given region of integration R and evaluate the integral over using polar coordinates. - dA; R = {(x,y): x² + y² ≤ 1, xz0, yz0} √9-x²2-² Sketch the given region of integration R. Choose the correct graph below. O A. dA= √9-x² R (Type an exact answer.) Q ✔ N O B. O C. D. Q
Sketch the given region of integration R and evaluate the integral over using polar coordinates. - dA; R = {(x,y): x² + y² ≤ 1, xz0, yz0} √9-x²2-² Sketch the given region of integration R. Choose the correct graph below. O A. dA= √9-x² R (Type an exact answer.) Q ✔ N O B. O C. D. Q
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![### Problem Statement
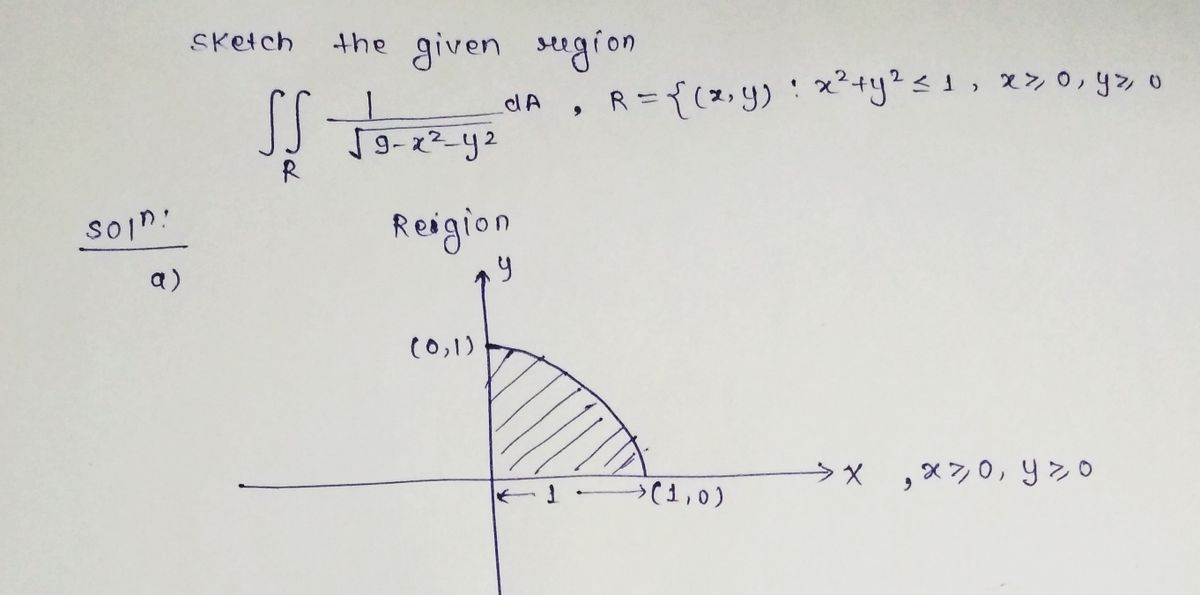
Sketch the given region of integration \( R \) and evaluate the integral over \( R \) using polar coordinates:
\[
\iint_R \frac{1}{\sqrt{9 - x^2 - y^2}} \, dA; \quad R = \{(x, y): x^2 + y^2 \leq 1, x \geq 0, y \geq 0\}
\]
---
### Instructions
Sketch the given region of integration \( R \). Choose the correct graph below.
- **Option A**: A semicircle in the upper half of the plane centered at the origin with radius 1.
- **Option B**: A full circle centered at the origin with radius 1.
- **Option C**: A semicircle on the right side of the plane centered at the origin with radius 1.
- **Option D**: A quarter circle in the first quadrant centered at the origin with radius 1. (Selected as correct)
---
### Solution
Evaluate the integral:
\[
\iint_R \frac{1}{\sqrt{9 - x^2 - y^2}} \, dA = \frac{3\pi}{2}
\]
(Type an exact answer.)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff2c370c8-f220-47ec-b561-9f6a07b2c79a%2Fd6576d24-26b2-4bbe-ac61-f16b3c8161a2%2Fikyw7ve_processed.png&w=3840&q=75)
Transcribed Image Text:### Problem Statement
Sketch the given region of integration \( R \) and evaluate the integral over \( R \) using polar coordinates:
\[
\iint_R \frac{1}{\sqrt{9 - x^2 - y^2}} \, dA; \quad R = \{(x, y): x^2 + y^2 \leq 1, x \geq 0, y \geq 0\}
\]
---
### Instructions
Sketch the given region of integration \( R \). Choose the correct graph below.
- **Option A**: A semicircle in the upper half of the plane centered at the origin with radius 1.
- **Option B**: A full circle centered at the origin with radius 1.
- **Option C**: A semicircle on the right side of the plane centered at the origin with radius 1.
- **Option D**: A quarter circle in the first quadrant centered at the origin with radius 1. (Selected as correct)
---
### Solution
Evaluate the integral:
\[
\iint_R \frac{1}{\sqrt{9 - x^2 - y^2}} \, dA = \frac{3\pi}{2}
\]
(Type an exact answer.)
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

