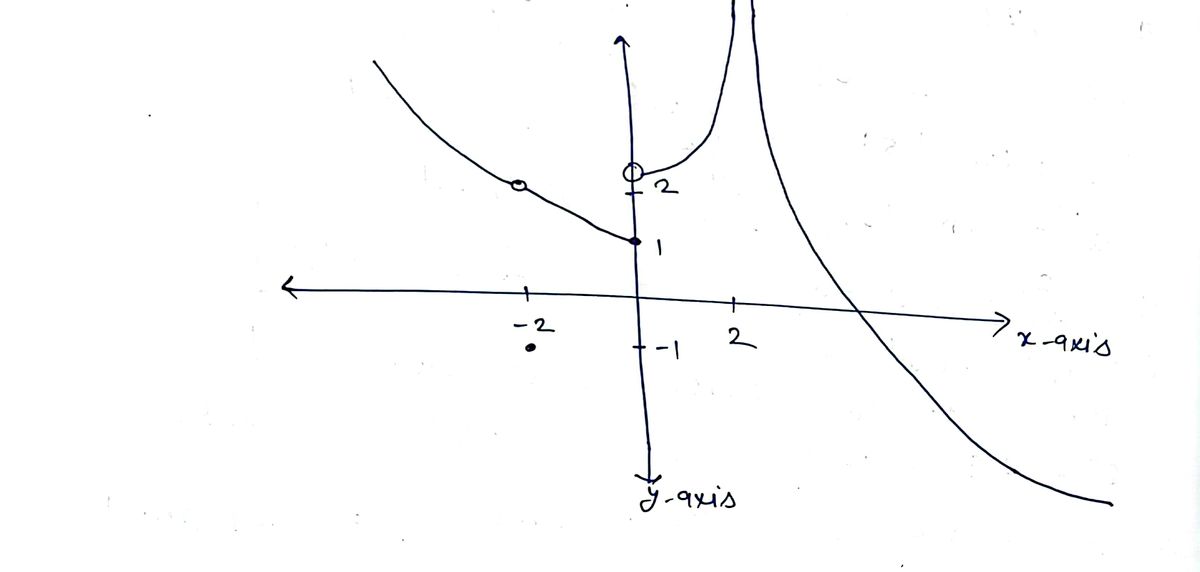
Sketch a function that has the following properties: lim f(x) = 2 *4-2 f(-2) = -1 lim f(x) DNE *→0 The domain of f is (-∞0, 2) U (2,00)
Sketch a function that has the following properties: lim f(x) = 2 *4-2 f(-2) = -1 lim f(x) DNE *→0 The domain of f is (-∞0, 2) U (2,00)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Sketch a Function with the Following Properties:**
1. \(\lim_{x \to 2} f(x) = 2\)
2. \(f(-2) = -1\)
3. \(\lim_{x \to 0} f(x)\) DNE
The domain of \(f\) is \((-\infty, 2) \cup (2, \infty)\).
---
**Graph Explanation:**
Below is a grid for sketching the function. The x-axis ranges from -5 to 5, and the y-axis ranges from -5 to 5. Each line on the grid is spaced at intervals of 1.
**Key Points to Consider:**
- As \(x\) approaches 2 from the left or right, \(f(x)\) approaches 2, suggesting a point or horizontal line approaching but not crossing or including 2 at \(x=2\).
- The point at \(x = -2\) is given by \(f(-2) = -1\). This is a specific point that should be clearly marked on the graph.
- The limit as \(x\) approaches 0 does not exist, indicating a discontinuity or asymptote at \(x=0\).
- The function is not defined exactly at \(x = 2\), and the domain is split into two intervals: all real numbers less than 2 or greater than 2.
*Note: You may upload a picture of your graph if you'd prefer to make it by hand.*
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

