Show that x +x² + 1 is irreducible over Z2. Let a be a zero of x + x2 + 1 in an extension field of Z2. Show that x3 +x2 +1 factors into three linear factors in (Z2(@))[x] by actually finding this factorization. [Hint: Every element of Z2(a) is of the form ao + aja + a2a for a; = 0, 1. Divide x3 + x²+1 by x – a by long division. Show that the quotient also has a zero in Z2(a) by simply trving the eight nossible elements. Then complete the factorization.]
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
![b. Finu a
E Of IR šuch that e² is algebraic of degree 5 over E.
25. a. Show that x+ x + 1 is irreducible over Z2.
b. Let a be a zero of x + x² +1 in an extension field of Z2. Show that x3+x² + 1 factors into three linear
factors in (Z2(a))[x] by actually finding this factorization. [Hint: Every element of Z2(a) is of the form
ao + aja + aza for a; = 0, 1.
Divide x + x² + 1 by x – a by long division. Show that the quotient also has a zero in Z2(@) by simply
trying the eight possible elements. Then complete the factorization.]
26. Let E be an extension field of Z2 and let a e E be algebraic of degree 3 over Z2. Classify the groups (Z2(@), +)
norom of finitely generated abelian groups. As usual, (Za(@)*](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb4dd8e23-ab66-4b24-8e54-a64daec9031c%2F8963736b-9f77-4777-a211-84214b19cd85%2Fip8gm2_processed.jpeg&w=3840&q=75)
(a)
The objective is to show that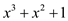 
is irreducible over 
.
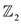Let 
.
If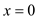 
, then,
If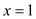 
, then,
So,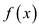 
has no zeros over 
.
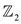Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 52 images
