Show that the following is true. cos(180° - 0) = -cos e
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Topic Video
Question
Please show me how to do this problem!
![**Verify the Trigonometric Identity**
Show that the following is true:
\[
\cos(180^\circ - \theta) = -\cos \theta
\]
### Explanation
This identity can be verified using the properties of the cosine function.
- The angle \( 180^\circ - \theta \) is in the second quadrant of the unit circle, where the cosine of an angle is negative.
- Using the reference angle, the cosine of \( 180^\circ - \theta \) is the negative of the cosine of \( \theta \).
This identity is an example of how trigonometric functions behave under angle transformations, specifically within different quadrants on the unit circle.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb49976cd-c3bf-478b-8ad4-67f602b8a4e2%2F63997828-f539-46e4-9550-dd1accecdd2f%2Fuzoz2gm_processed.png&w=3840&q=75)
Transcribed Image Text:**Verify the Trigonometric Identity**
Show that the following is true:
\[
\cos(180^\circ - \theta) = -\cos \theta
\]
### Explanation
This identity can be verified using the properties of the cosine function.
- The angle \( 180^\circ - \theta \) is in the second quadrant of the unit circle, where the cosine of an angle is negative.
- Using the reference angle, the cosine of \( 180^\circ - \theta \) is the negative of the cosine of \( \theta \).
This identity is an example of how trigonometric functions behave under angle transformations, specifically within different quadrants on the unit circle.
Expert Solution
Step 1
You know the formula:
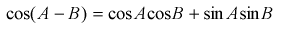
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning