Show that if (r) has mean momentum (P) then e(r) has mean momentum (P) + Po.
Related questions
Question

Transcribed Image Text:**Problem Statement:**
"Show that if \( \psi(x) \) has mean momentum \( \langle P \rangle \), then \( e^{iP_0x/\hbar} \psi(x) \) has mean momentum \( \langle P \rangle + P_0 \)."
**Explanation:**
This statement is related to quantum mechanics, exploring how a wave function \( \psi(x) \) with a given mean momentum can be altered by a phase factor \( e^{iP_0x/\hbar} \). Adding this phase modifies the mean momentum of the state to \( \langle P \rangle + P_0 \). This illustrates a principle where multiplying by a phase factor corresponds to a shift in momentum space.
Expert Solution
Step 1: Problem Statement
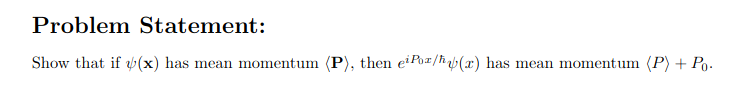
Step by step
Solved in 3 steps with 4 images
