Show that if mod (n, 4) = 1, then y must be even. Show that if mod (n, 4) = 3, then y must be odd.
Show that if mod (n, 4) = 1, then y must be even. Show that if mod (n, 4) = 3, then y must be odd.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please do Exercise 9.3.13 part D and E show step by step and please explain.
Hints:
Hint for (a) Prove by contradiction.
Hint for (b) Write m = 2k+1.
Hint for (d) Use part (c), part (b), and the distributive law.
Hint for (e) This is similar to part(b).

Transcribed Image Text:where both x and y are greater than 1. Consequently, a positive odd integer
can be factored exactly when we can find integers x and y such that n =
x² - y². (*Hint*)
We can use this fact to factor n by trying different pairs of squares in
order to get n as the difference of the two. Of course, we want to do this
systematically. So we want to see what values of r and y we actually need
to check:
Exercise 9.3.12. In the formula n = x² - y² = (x − y)(x + y), what is the
smallest possible value for r that needs to be tested? (*Hint*)
There are other special conditions that r and y must satisfy:
Exercise 9.3.13.
(a) Assuming that n is an odd number, show that if x is odd then y is even,
and if x is even then y is odd. (*Hint*)
(b) Show that for any odd number m, then mod (m², 4) = 1. (*Hint*)
(c) Let m = x + y. Show that m is odd, and that we can rewrite n =
(x−y)(x+y) as: n = m(m - 2y).
(d) Show that if
mod (n. 4) = 1, then y must be even. (*Hint*)
(e) Show that if mod (n, 4) = 3, then y must be odd. (*Hint*)
The Fermat primality testing scheme is better for finding factors that
are nearly equal. The brute force method of Exercise 9.3.14 is much better
when one factor is much bigger than the other one.

Transcribed Image Text:Fermat's test for primality
Even using various tricks to reduce the number of computations, the brute
force method requires far too many calculations to be useful for RSA encod-
ing. A different algorithm for testing primality is Fermat's factorization
algorithm, which depends on the following fact:
Exercise 9.3.11. Let n = ab be an odd composite number where a, b € N.
Prove that n can be written as the difference of two perfect squares :
n = x² - y² = (x - y) (x + y),
Expert Solution
Step 1
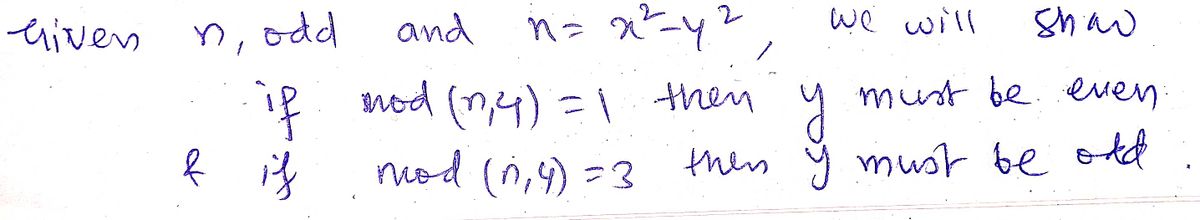
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

