Show all steps and give appropriate justifications. Simplify your answers whenever possible. 1. Solve the IVP y(3) – y" = 6x + 2e", y(0) = 0, y'(0) = 4, y"(0) : 2. Find a particular solution of y" + 16y = sin(4.x)+ sec²(4x)

Hi! You have posted multiple questions. As per norms, we will be solving only one question. We will be solving the first question as nothing is specified. If you need the answer to another question then kindly re-submit the question by specifying the required question.   

Here, we are given the IVP,

            .

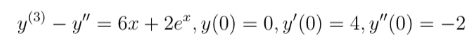Note: 

So, first, we will find the solution to the corresponding homogeneous equation.

The characteristic equation is,

                                          m³ - m² = 0

                                    => m²(m-1) = 0

                                    => m = 0, 0, 1.

Thus, y_c = c₁ + c₂x + c₃e^x.

Let us solve this differential equation by the method of undetermined coefficients.

Here, g(x) = 6x + 2e^x.

For 6x, the possible choice of solution is A+Bx. But x is already solving the corresponding homogeneous solution.

So, now we multiply by x to the choice.

Then, for 6x, the possible choice of solution is Ax+Bx². But again x is already solving the corresponding homogeneous solution.

So, now we multiply by x to the choice.

Then finally, for 6x, the possible choice of solution is Ax²+Bx³.

Now, the possible choice of solution is Ce^x. But e^x is already solving the corresponding homogeneous solution.

So, now we multiply by x to the choice.

Then finally, for e^x, the possible choice of solution is Cxe^x.

Thus, y_p = Ax²+Bx³+Cxe^x.

Now, we need to find the constants A, B, and C.