Answered: Scores on a large standardized test are…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Topic Video

Question

100%

Scores on a large standardized test are normally distributed with a national average score of 75. At a college, we have 16 students who take this test and get an average score of 76 with a standard deviation of 11. Use a significance level of 0.05.

What is the Null Hypothesis?

What is the Alternate Hypothesis?

What is the Test Statistic?

Features Features Normal distribution is characterized by two parameters, mean (µ) and standard deviation (σ). When graphed, the mean represents the center of the bell curve and the graph is perfectly symmetric about the center. The mean, median, and mode are all equal for a normal distribution. The standard deviation measures the data's spread from the center. The higher the standard deviation, the more the data is spread out and the flatter the bell curve looks. Variance is another commonly used measure of the spread of the distribution and is equal to the square of the standard deviation.

Expert Solution

Step 1

Given Information :

The provided sample mean is $\bar{x}$ $= 76$ and the sample standard deviation is $s = 11$ , and the sample size is $n = 16$ .

Null and Alternative Hypotheses

The following null and alternative hypotheses need to be tested:

Ho: College average score is equal to national average score .

$μ$ = $75$

Ha: College average score is different than the national average score .

$μ$ ≠ $75$

This corresponds to a two-tailed test, for which a t-test for one mean, with unknown population standard deviation will be used.

Step 2

Rejection Region

Based on the information provided, the significance level is $\alpha = 0.05$ , and the critical value for a two-tailed test is $t_{c} = 2.131$ .

The rejection region for this two-tailed test is $R = \{t: |t| > 2.131\}$

Test Statistics

The t-statistic is computed as follows:

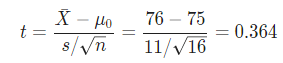
Test Statistic = 0.364

Step by step

Solved in 3 steps with 1 images

Knowledge Booster

$Hypothesis Tests and Confidence Intervals for Means$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions