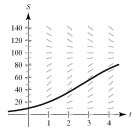
Answered: S 140 120 100 1 2 4 /// ||\\\\\\\ ///…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Concept explainers

Question

Let S represent sales of a new product (in thousands of units), let L represent the maximum level of sales (in thousands of units), and let t represent time (in months). The rate of change of S with respect to t is proportional to the product of S and L − S.

(a) Write the differential equation for the sales model when L = 100, S = 10 when t = 0, and S = 20 when t = 1.

Verify that S =L/( 1 + Ce^−kt).

(b) At what time is the growth in sales increasing most rapidly?

(d) Sketch the solution from part (a) on the slope field below. To print an enlarged copy of the graph, go to MathGraphs.com. Assume the estimated aximum level of sales is correct. Use the slope field to describe the shape of the solution curves for sales when, at some period of time, sales exceed L.

S
140
120
100
1
2
4
/// ||\\\\\\\
/// ||\\\\\\|
/// ||\\\\\\\ |
/// ||\\\\\\|

Expert Solution

Step 1

Introduction :

Sales in math deals with rough estimating at times and it gives that big picture view needed to make major business decisions in selling efforts.

Given :

Let $S$ represent sales of a new product (in thousands of units), let $L$ represent the maximum level of sales (in thousands of units), and let $t$ represent time (in months). The rate of change of $S$ with respect to $t$ is proportional to the product of $S$ and $L - S$ .

Objective :

$(a)$ To write the differential equation for the sales model when $L = 100, S = 10$ when $t = 0$ , and $S = 20$ when $t = 1$ .

and verify that $S = \frac{L}{(1 + C e^{- k t})}$ .

$(b)$ To determine at what time is the growth in sales increasing most rapidly?

$(c)$ To use a graphing utility to graph the sales function.

$(d)$ To sketch the solution from part $(a)$ on the slope field below.

Step 2

(a)

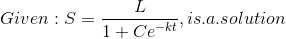
Differentiating S with respect to t

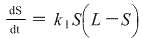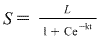is a solution because

Differentiating S with respect to t

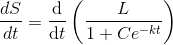
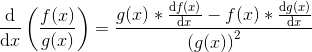
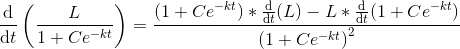
L is constant.

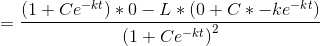
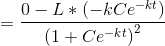
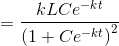
we divide and multiply by L

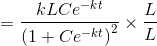
We split the whole equation into

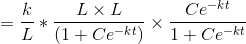
k/L is a constant . Let it be together denoted by a constant k1

Adding 1 and subtracting 1 for simplification

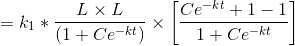
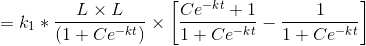
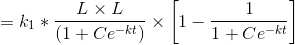
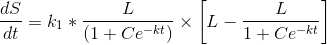
Now for particular solution

L= 100 remains constant

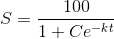
1. When L = 100 , S = 10 , t=0

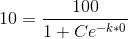
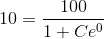
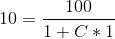
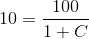
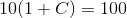
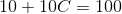
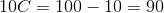
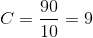
Substituting value of C in main solution , the particular solution is

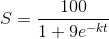
When L = 100 , S = 20 , t=1

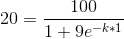
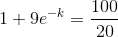
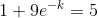
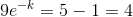
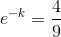
Taking natural logarithm on both sides

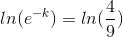
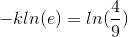
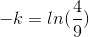
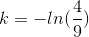
Substituting value in previous equation

(b)

Find the time at which the growth in sales is increasing most rapidly. So,

Choosing S = 50,

Solving for t gives

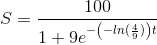
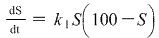
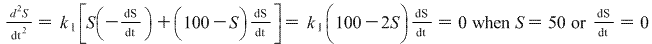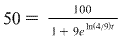
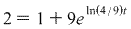
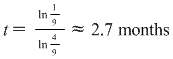(This is an inflection point)

(c)

Here is the graph of the sales function:

(d)

Here is the sketch of the solution from part

(a)

on the given slope field:

Step by step

Solved in 3 steps with 45 images

Knowledge Booster

$Differential Equation$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions