Remembering that any complex number can be written in the form re" by (9.4), we get Section 9 Euler's Formula 63 2 e2 = ri r2 e4(02+@2), e 21 22 (9.6) In words, to multiply two complex numbers, we multiply their absolute values and add their angles. To divide two complex numbers, we divide the absolute values and subtract the angles Example. Evaluate (1 + i)?/(1 - i). From Figure 5.1 we have 1 2et/4. We plot 1 - i in Figure 9.5 and find r2, 0=/4 (or +7/4), so 1-i= /2e-i#/4. Then (VEetr/a)2 V2e-i7/4=J%-in/s = /2e3i#/4 2 eir/2 (1+i)2 1-1 Figure 9.5 From Figure 9.6, we find =-1, y = 1, so (1i)2 1-1 =riy-1+i We could use degrees in this problem. By (9.6), we find that the angle of (1 i)2/(1-i) is 2(45°) - (-45°) 135° as in Figure 9.6 Figure 9.6 PROBLEMS, SECTION 9 Express the following complex numbers in the r + iy form. Try to visualize each complex number, using sketches as in the examples if necessary. The first twelve problems you should be able to do in your head (and maybe some of the others-try it!) Doing a problem quickly in your head saves time over using a computer. Remember that the point in doing problems like this is to gain skill in manipulating complex expressions, so a good study method is to do the problems by hand and use a computer to check your answers. 3. 93ri/2 e-2i -4mi - 2. ei/2 1. ei/4 (a/3)(344mi 4. 6. 5. 7. 3e2(1+i 2esri/6 9. 2e-i/2 /4 4e-Sin/3 10. 11. 12. (i) 1-i (1+ W) 15. (1 (1 i)* 14. 13. ( (-)(1+v) 17. 16 () 19. (1-) 21 20.

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Concept explainers

Topic Video

Question

Problems, Section 9 number 8,10,11,13. Please answer the questions

Remembering that any complex number can be written in the form re" by (9.4),
we get
Section 9
Euler's Formula
63
2 e2 = ri r2 e4(02+@2),
e
21 22
(9.6)
In words, to multiply two complex numbers, we multiply their absolute values
and add their angles. To divide two complex numbers, we divide the absolute
values and subtract the angles
Example. Evaluate (1 + i)?/(1 - i). From Figure 5.1 we have
1 2et/4. We plot 1 - i in Figure 9.5 and find
r2, 0=/4 (or +7/4), so 1-i= /2e-i#/4. Then
(VEetr/a)2
V2e-i7/4=J%-in/s = /2e3i#/4
2 eir/2
(1+i)2
1-1
Figure 9.5
From Figure 9.6, we find =-1, y = 1, so
(1i)2
1-1
=riy-1+i
We could use degrees in this problem. By (9.6), we find
that the angle of (1 i)2/(1-i) is 2(45°) - (-45°) 135°
as in Figure 9.6
Figure 9.6
PROBLEMS, SECTION 9
Express the following complex numbers in the r + iy form. Try to visualize each complex
number, using sketches as in the examples if necessary. The first twelve problems you
should be able to do in your head (and maybe some of the others-try it!) Doing a
problem quickly in your head saves time over using a computer. Remember that the point
in doing problems like this is to gain skill in manipulating complex expressions, so a good
study method is to do the problems by hand and use a computer to check your answers.
3. 93ri/2
e-2i -4mi -
2. ei/2
1. ei/4
(a/3)(344mi
4.
6.
5.
7. 3e2(1+i
2esri/6
9.
2e-i/2
/4
4e-Sin/3
10.
11.
12.
(i)
1-i
(1+ W)
15. (1 (1 i)*
14.
13.
(
(-)(1+v)
17.
16
()
19. (1-)
21
20.

Expert Solution

Step 1

Hey, since there are multiple questions posted, we will answer first question. If you want any specific question to be answered then please submit that question only or specify the question number in your message.

Step 2

Problem 8:

A complex number in x+iy form is written as follows.

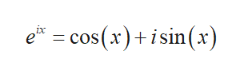
Step by step

Solved in 3 steps with 2 images

Knowledge Booster

$Propositional Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions