Could you explain how to show this in detail? Recall that the Euclidean scalar product in R² is defined by(x1, Y1) · (x2, Y2) := x1x2+ Y1 Y2 ·(i) Show that, setting z1 = x1+ iy1 and z2 = x2+ iy2, it holds21 · Z2 = Re (21z2).(ii) Show that, in the situation of Exercise 1 and with (1) enforced it holdsAz · Awforevery z, w E C\{0}.|Az||Aw||z||w|(Hint: Use (v) of Exercise 1). Discuss the geometric meaning of the above identity.

Name: Could you explain how to show this in detail? Recall that the Euclidea
Uploaded: 2024-03-20T06:38:44.000Z
Channel: Bartleby
Description: Could you explain how to show this in detail? Recall that the Euclidean scalar product in R² is defined by(x1, Y1) · (x2, Y2) := x1x2+ Y1 Y2 ·(i) Show that, setting z1 = x1+ iy1 and z2 = x2+ iy2, it holds21 · Z2 = Re (21z2).(ii) Show that, in the sit

Answered: Recall that the Euclidean scalar…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Concept explainers

Topic Video

Question

100%

Could you explain how to show this in detail?

Recall that the Euclidean scalar product in R² is defined by
(x1, Y1) · (x2, Y2) := x1x2+ Y1 Y2 ·
(i) Show that, setting z1 = x1+ iy1 and z2 = x2+ iy2, it holds
21 · Z2 = Re (21z2).
(ii) Show that, in the situation of Exercise 1 and with (1) enforced it holds
Az · Aw
for
every z, w E C\{0}.
|Az||Aw|
|z||w|
(Hint: Use (v) of Exercise 1). Discuss the geometric meaning of the above identity.

Expert Solution

Step 1

Since you have posted multiple questions but according to guidelines, we will solve first question for you. For rest of the questions resubmit the question again and specify the question you want us to solve.

Consider the given information:

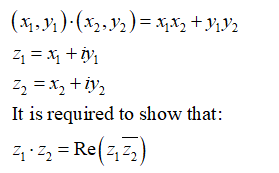
Step by step

Solved in 2 steps with 2 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Propositional Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions