Arc Length
Arc length can be thought of as the distance you would travel if you walked along the path of a curve. Arc length is used in a wide range of real applications. We might be interested in knowing how far a rocket travels if it is launched along a parabolic path. Alternatively, if a curve on a map represents a road, we might want to know how far we need to drive to get to our destination. The distance between two points along a curve is known as arc length.
Line Integral
A line integral is one of the important topics that are discussed in the calculus syllabus. When we have a function that we want to integrate, and we evaluate the function alongside a curve, we define it as a line integral. Evaluation of a function along a curve is very important in mathematics. Usually, by a line integral, we compute the area of the function along the curve. This integral is also known as curvilinear, curve, or path integral in short. If line integrals are to be calculated in the complex plane, then the term contour integral can be used as well.
Triple Integral
Examples:
Suppose C is the boundary of region R = {(x, y): x2 ≤ y ≤ x ≤ 1}, oriented counterclockwise (see figure); let F = ⟨1, x⟩.
a. Compute the two-dimensional curl of F and determine whether
F is irrotational.
b. Find parameterizations r1(t) and r2(t) for C1 and C2, respectively.
c. Evaluate both the line integral and the double integral in the circulation
form of Green’s Theorem and check for consistency.
d. Compute the two-dimensional divergence of F and use the flux
form of Green’s Theorem to explain why the outward flux is 0.

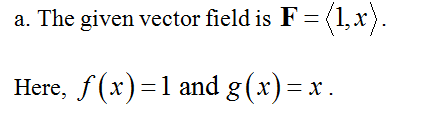


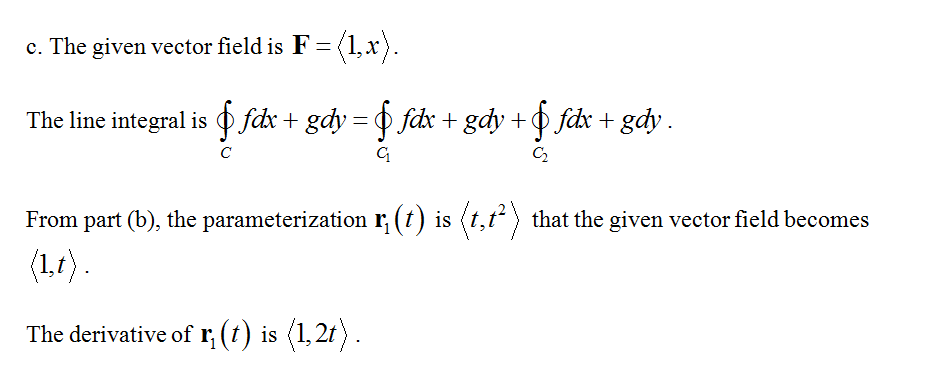

Step by step
Solved in 10 steps with 10 images









