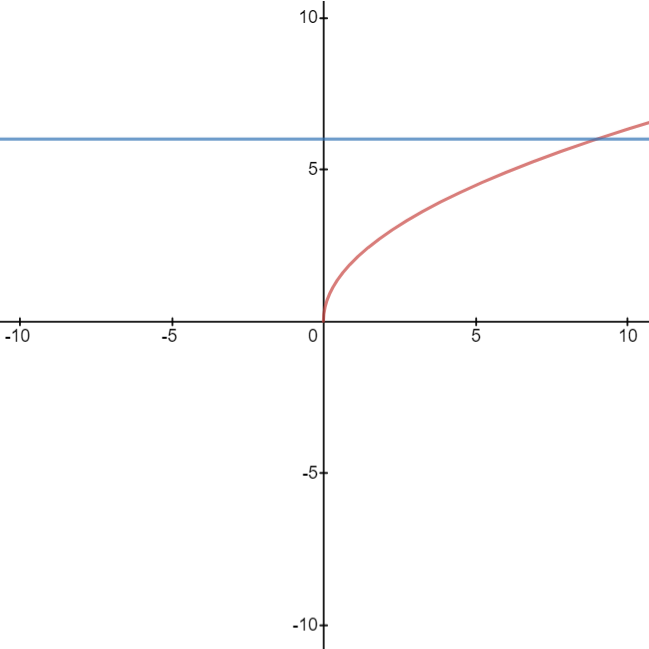
R be the region in the first quadrant bounded t axis, as shown in the figure above. Find the area of R. Write, but do not evaluate, an integral express rotated about the horizontal line y = 7. Region R is the base of a solid. For each y, w perpendicular to the y-axis is a rectangle whos but do not evaluate, an integral expression tha
R be the region in the first quadrant bounded t axis, as shown in the figure above. Find the area of R. Write, but do not evaluate, an integral express rotated about the horizontal line y = 7. Region R is the base of a solid. For each y, w perpendicular to the y-axis is a rectangle whos but do not evaluate, an integral expression tha
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
I need help with 4

Transcribed Image Text:Certainly! Here is the transcribed text that you might find on an educational website:
---
**Topic: Calculus – Applications of Integration**
4. **Problem Statement:**
Let \( R \) be the region in the first quadrant bounded by the graph of \( y = 2 \sqrt{x} \), the horizontal line \( y = 6 \), and the y-axis, as shown in the figure above.
**Tasks:**
(a) Find the area of \( R \).
(b) Write, but do not evaluate, an integral expression that gives the volume of the solid generated when \( R \) is rotated about the horizontal line \( y = 6 \).
(c) Region \( R \) is the base of a solid. For each \( y \), where \( 0 \leq y \leq 6 \), the cross-section of the solid taken perpendicular to the y-axis is a rectangle whose height is 3 times the length of its base in region \( R \). Write, but do not evaluate, an integral expression that gives the volume of the solid.
**Illustration:**
The diagram is a graph showing the curve \( y = 2 \sqrt{x} \) and the line \( y = 6 \), creating a shaded region \( R \) in the first quadrant adjacent to the y-axis. The x-axis and y-axis create boundaries, with the shaded area bound between the curve and the horizontal line at \( y = 6 \).
---
This transcription provides a clear explanation and representation of the mathematical problem, which can help students understand the concepts of area and volume in calculus based on the given figure.
Expert Solution
Step 1
given
a curve
a horizontal line
to find
(a) area of the region
Step 2
explanation
graph of the region
Step by step
Solved in 4 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

