(c) Calculate the values of the residuals from the least squares line for the four observations for which temperature is 186. Why do they not all have the same sign? The four observations for which temperature is 186, written as ordered pairs, are: (186, 0.89), (186, 1.86), (186, 2.03), and (186, 2.69). Recall the residual from the least squares line is the difference between the observed and predicted values. In part (b), we calculated the predicted value for a tank temperature of 186 to be 1.9057. Use this value to calculate the residuals for each of the four observations, rounded to two decimal places. (186, 0.89): 0.89 1.9057 -1.02 (186, 1.86): 1.86 1.9057 -0.05 (186, 2.03): 2.03 - 1.9057 = (186, 2.69): 2.69 -1.9057 = These residuals do not all have the same sign because in the first two observations listed, the observed efficiency ratios were ---Select-- For the third and fourth observations, the observed efficiency ratios were ---Select--than the predicted value, resulting in ---Select--- Submit Skip (you cannot come back) than the predicted value, resulting in ---Select--- residuals. residuals.
(c) Calculate the values of the residuals from the least squares line for the four observations for which temperature is 186. Why do they not all have the same sign? The four observations for which temperature is 186, written as ordered pairs, are: (186, 0.89), (186, 1.86), (186, 2.03), and (186, 2.69). Recall the residual from the least squares line is the difference between the observed and predicted values. In part (b), we calculated the predicted value for a tank temperature of 186 to be 1.9057. Use this value to calculate the residuals for each of the four observations, rounded to two decimal places. (186, 0.89): 0.89 1.9057 -1.02 (186, 1.86): 1.86 1.9057 -0.05 (186, 2.03): 2.03 - 1.9057 = (186, 2.69): 2.69 -1.9057 = These residuals do not all have the same sign because in the first two observations listed, the observed efficiency ratios were ---Select-- For the third and fourth observations, the observed efficiency ratios were ---Select--than the predicted value, resulting in ---Select--- Submit Skip (you cannot come back) than the predicted value, resulting in ---Select--- residuals. residuals.
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
answer the blank please and the "These residuals do not all have the same sign because in the first two observations listed, the observed efficiency ratios were" ty!

Transcribed Image Text:(c) Calculate the values of the residuals from the least squares line for the four observations for which temperature is 186. Why do they not all have the same sign?
The four observations for which temperature is 186, written as ordered pairs, are:
(186, 0.89), (186, 1.86), (186, 2.03), and (186, 2.69).
Recall the residual from the least squares line is the difference between the observed and predicted values. In part (b), we calculated the predicted value for a tank temperature of 186 to be 1.9057. Use
this value to calculate the residuals for each of the four observations, rounded to two decimal places.
(186, 0.89): 0.89
(186, 1.86): 1.86
(186, 2.03): 2.03
(186, 2.69): 2.69
1.9057 = -1.02
1.9057= -0.05
1.9057 =
1.9057
Submit
=
These residuals do not all have the same sign because in the first two observations listed, the observed efficiency ratios were --Select---
For the third and fourth observations, the observed efficiency ratios were --Select--- than the predicted value, resulting in ---Select---
Skip (you cannot come back)
than the predicted value, resulting in -Select--- residuals.
residuals.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
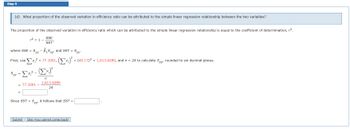
Transcribed Image Text:Step 9
(d) What proportion of the observed variation in efficiency ratio can be attributed to the simple linear regression relationship between the two variables?
The proportion of the observed variation in efficiency ratio which can be attributed to the simple linear regression relationship is equal to the coefficient of determination, r².
r² = 1-
SSE
SST'
where SSE = Syy - B₁Sxy, and SST = Syy.
First, use v² = 77.1001, (v₁)² = (40.17)² = 1,613.6289, and n = 24 to calculate Sy
yy'
Swy = y? -
= 77.1001
n
Since SST = S,
1,613.6289
24
Syy, it follows that SST =
Submit Skip (you cannot come back)
rounded to six decimal places.
Solution
Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
