Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
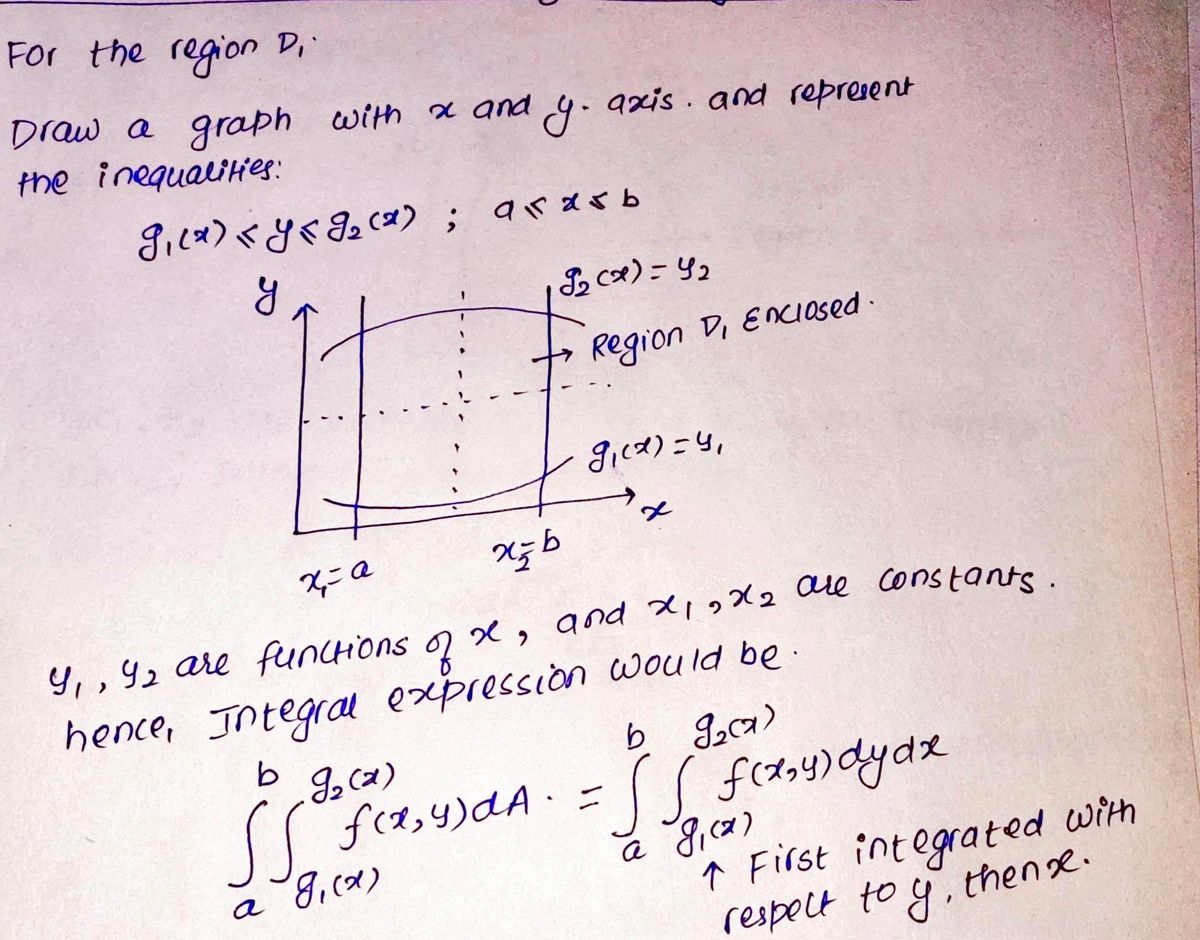
QUESTION 6 If the region D, can be described by the inequalities g, (x) ≤ y ≤ g₂ (x) and a ≤ x ≤ b, where g₁ = 9₁(x) and g₂= 9₂(x) are functions of only x, then SD, f(x,y) dA= Alternatively, if the region D is described by the inequalities h, (v) ≤x≤h, (v) and, csysd. where h₂= h, (y) and h₂ h₂(y) are functions of only y, we have SD, f(x,y) dA= D₂ Write the iterated integrals D, and D₂.

QUESTION 6 If the region D, can be described by the inequalities g, (x) ≤ y ≤ g₂ (x) and a ≤ x ≤ b, where g₁ = 9₁(x) and g₂= 9₂(x) are functions of only x, then SD, f(x,y) dA= Alternatively, if the region D is described by the inequalities h, (v) ≤x≤h, (v) and, csysd. where h₂= h, (y) and h₂ h₂(y) are functions of only y, we have SD, f(x,y) dA= D₂ Write the iterated integrals D, and D₂.

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
QUESTION 6 If the region D, can be described by the inequalities g, (x) ≤ y ≤ g₂ (x) and a ≤ x ≤ b, where g₁ = 9₁(x) and g₂ = 9₂(x) are functions of only ,x, then D, f(x,y) dA= Alternatively, if the region D is described by the inequalities h, (y) ≤ x ≤ h₂(y) and, c≤ y ≤d, where h₁ = h, (y) and h₂ h₂(y) are functions of only y, we have SD, f(x,y) dA= D₂ Write the iterated integrals D, and D₂.
Transcribed Image Text:QUESTION 6 If the region D, can be described by the inequalities g, (x) ≤ y ≤ g₂ (x) and a ≤ x ≤ b, where g₁ = 9₁(x) and g₂ = 9₂(x) are functions of only ,x, then D, f(x,y) dA= Alternatively, if the region D is described by the inequalities h, (y) ≤ x ≤ h₂(y) and, c≤ y ≤d, where h₁ = h, (y) and h₂ h₂(y) are functions of only y, we have SD, f(x,y) dA= D₂ Write the iterated integrals D, and D₂.
Expert Solution
Step 1

Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Similar questions
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS