Q9 charge. (i) Find the electric field a distance b (Fig. E2) from an infinitely long wire that carries a uniform line (4) (ii) E = E = 21 80 2 2πε b (iii) E=0 (iv) E= 19 276 rh (v) None of the other mentioned options b ww 1 Gaussian surface Fig. E2

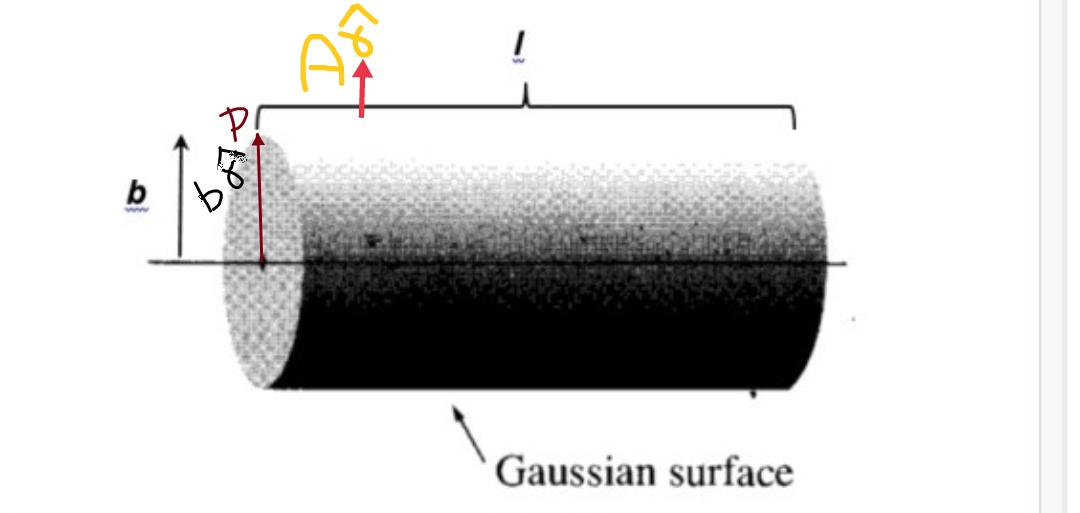
Consider an infinitely long straight, uniformly charged wire as shown above. Let the linear charge density of this wire be λ. P is the point that is located at a perpendicular distance from the wire. The distance between point P and the wire is b as shown in figure.
The wire is considered to be a cylindrical Gaussian surface. This is because to determine the electric field E at point P cylindrical surface is an ideal for Gauss law to be used.
The surface area of the curved part is given as:
S = 2πbl
The total charge enclosed by the gaussian surface is given as:
q = λl
The electric flux through the end surfaces of the cylindrical Gaussian surface is given as:
Φ1 = 0 because the electric field is supposed to be parallel to this plane and perpendicular to the curved surfaces only.
The electric flux through the curved surface of the cylindrical Gaussian surface is given as:
Φ2 = E .(Area vector of curved surface)
Φ2 =( E .(Area of curved surface))cosθ
Since area vector = s =2πbl r^
So both electric field and area vectors are parallel and directed radially outward
cosθ=1
Φ2 = E x 1 x 2πbl
The total electric flux is given as:
Φ = Φ1 + Φ2
Φ = 0 + E cosθ.s
Φ2 = 2πblE
Φ = 2πblE
From Gauss law of electrostatics, we know that ,
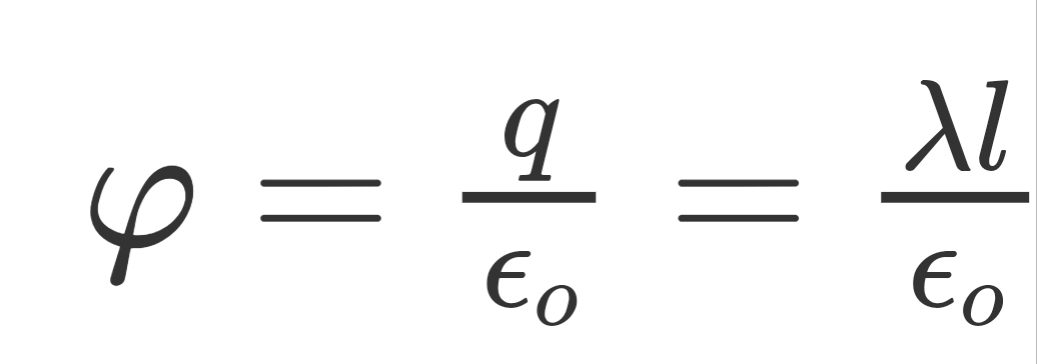
2πblE=(λl/ε0)
E=(λ/2πε0)×(1/b)
Step by step
Solved in 2 steps with 3 images









