Q1. Particle size distribution of a sample of spherical particles is represented by the differential frequency distribution qn(d) which is a function of particle diameter d with the graph shown below. 9n(d) (µm-1) 0 0 (a) Calculate the value of qn(0). 250 d (μm) (b) Calculate values of the cumulative frequency distribution Qn(d) for the following values of d (in µm): 25, 125 and 225. (c) Calculate the length weighted mean diameter and the surface weighted mean diameter of particles in the sample.
Q1. Particle size distribution of a sample of spherical particles is represented by the differential frequency distribution qn(d) which is a function of particle diameter d with the graph shown below. 9n(d) (µm-1) 0 0 (a) Calculate the value of qn(0). 250 d (μm) (b) Calculate values of the cumulative frequency distribution Qn(d) for the following values of d (in µm): 25, 125 and 225. (c) Calculate the length weighted mean diameter and the surface weighted mean diameter of particles in the sample.
Introduction to Chemical Engineering Thermodynamics
8th Edition
ISBN:9781259696527
Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Publisher:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Chapter1: Introduction
Section: Chapter Questions
Problem 1.1P
Related questions
Question
100%
Q1. (a) 8 x 10-3 um-1
(b) 0.19, 0.75 and 0.99
(c) 125 um and 150 um
(d) 1.22 x 106 particles and 0.04 m2

Transcribed Image Text:Relative frequency: f₁ = f(x)x₁,<x5x₁ = Q(x,) - Q(x₁) =
Cumulative frequency distribution: Q(x)
Differential frequency distribution: q(x):
Weighted mean size: x =
Number weighted mean size: M₁/Mo
Length weighted mean size: μ₂/M₁
Surface weighted mean size: μ3/μ₂
Volume weighted mean size: μ4/M3
Total volume of all particles:
W₁
St =
Nbins
S₁
=
Nins
-
n-th moment of particle size distribution: A4, =
Ni
Nin
Σw, x, [N, wx, [ƒ, wx, [w(x) xq (x) dx
i=1
Tw(x) q₁ (x)dx
i=1
Amount of particles with size ≤ x
Amount of all particles
dQ(x)
dx
ΣN,W
i=1
Nbins
• Σ N₁ (= ma² + xd₁L) = N(
i=1
=
Nbins
=[ N₁ (²nd² + 7dL₁) = N
=
лdL;
i=1
Ĵq(x)dx
i=1
~(ESX
x
or q (x₁)
i=1
Nhi
ΣΗ
i=1
Vs = ΣN₁Bx² = BN x³ qn(x) dx
fiw,
Total surface area of all particles (for cube and sphere shapes):
Nbins
S₁ = Σ N₁ax? = aN
i=1
f₁x" = √x"q, (x) dx
X
Total surface area of all particles (for cylinder shapes with constant L):
Anh da
x qn (x)
Total surface area of all particles (for cylinder shapes with constant d):
≈
[x² qn(x) dx
√ x²
Q(xi+1)-Q(xi)
Xi+1-Xi
x² qn(x) dx + L
+ N(57d² + md [ x 9₁ (x) dx)
S
qn

Transcribed Image Text:Q1. Particle size distribution of a sample of spherical particles is represented by
the differential frequency distribution qn(d) which is a function of particle diameter
d with the graph shown below.
an(d)
(μm-1)
0
0
(a) Calculate the value of qn(0).
250
d (μm)
(b) Calculate values of the cumulative frequency distribution Qn(d) for the
following values of d (in µm): 25, 125 and 225.
(c) Calculate the length weighted mean diameter and the surface weighted mean
diameter of particles in the sample.
(d) Calculate the total number and total surface area of particles in 1 cm³ of the
sample.
(e) Consider a gas laden with particles which exhibit the size distribution given in
this question. Describe how you could separate the particles from the gas.
Explain your reasoning.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 18 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
where does the 3.2x10-5 come from ?
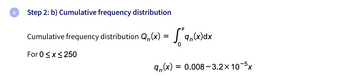
Transcribed Image Text:Step 2: b) Cumulative frequency distribution
Cumulative frequency distribution Q₁,(x) = 9,(x)dx
For 0 ≤ x ≤ 250
= 0.008-3.2x 10-5x
9n(x):
Solution
Recommended textbooks for you

Introduction to Chemical Engineering Thermodynami…
Chemical Engineering
ISBN:
9781259696527
Author:
J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Publisher:
McGraw-Hill Education

Elementary Principles of Chemical Processes, Bind…
Chemical Engineering
ISBN:
9781118431221
Author:
Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard
Publisher:
WILEY

Elements of Chemical Reaction Engineering (5th Ed…
Chemical Engineering
ISBN:
9780133887518
Author:
H. Scott Fogler
Publisher:
Prentice Hall

Introduction to Chemical Engineering Thermodynami…
Chemical Engineering
ISBN:
9781259696527
Author:
J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Publisher:
McGraw-Hill Education

Elementary Principles of Chemical Processes, Bind…
Chemical Engineering
ISBN:
9781118431221
Author:
Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard
Publisher:
WILEY

Elements of Chemical Reaction Engineering (5th Ed…
Chemical Engineering
ISBN:
9780133887518
Author:
H. Scott Fogler
Publisher:
Prentice Hall


Industrial Plastics: Theory and Applications
Chemical Engineering
ISBN:
9781285061238
Author:
Lokensgard, Erik
Publisher:
Delmar Cengage Learning

Unit Operations of Chemical Engineering
Chemical Engineering
ISBN:
9780072848236
Author:
Warren McCabe, Julian C. Smith, Peter Harriott
Publisher:
McGraw-Hill Companies, The