prove Vlx-yl < √lx-rl + √r-x] where x,y,re
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Objective:**
Prove the inequality:
\[
\sqrt{|x - y|} \leq \sqrt{|x - r|} + \sqrt{|r - x|}
\]
where \(x, y, r \in \mathbb{R}\).
**Explanation:**
This mathematical expression is an inequality involving real numbers \(x\), \(y\), and \(r\). The task is to demonstrate that the square root of the absolute difference between \(x\) and \(y\) is less than or equal to the sum of the square roots of the absolute differences between \(x\) and \(r\), and \(r\) and \(x\).
**Key Concepts:**
- **Absolute Value:** The absolute value of a number is its distance from zero on a number line, regardless of direction. It is denoted as \(|a|\).
- **Square Root:** A square root of a number \(a\) is a value that, when multiplied by itself, gives \(a\).
- **Inequality Proofs:** Demonstrating that one side of an equation or inequality is consistently smaller or equal to another under defined conditions.
This problem can involve exploring algebraic manipulations or properties of inequalities to establish the stated relation. Additionally, one may need to consider the properties of metric spaces and the triangle inequality if dealing with potential complex formulations.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fbdd7eaed-9b44-4003-81eb-7e8fab9c2687%2Fd5f30e7c-4339-4227-a15d-d000155f8903%2Fb8htvj_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Objective:**
Prove the inequality:
\[
\sqrt{|x - y|} \leq \sqrt{|x - r|} + \sqrt{|r - x|}
\]
where \(x, y, r \in \mathbb{R}\).
**Explanation:**
This mathematical expression is an inequality involving real numbers \(x\), \(y\), and \(r\). The task is to demonstrate that the square root of the absolute difference between \(x\) and \(y\) is less than or equal to the sum of the square roots of the absolute differences between \(x\) and \(r\), and \(r\) and \(x\).
**Key Concepts:**
- **Absolute Value:** The absolute value of a number is its distance from zero on a number line, regardless of direction. It is denoted as \(|a|\).
- **Square Root:** A square root of a number \(a\) is a value that, when multiplied by itself, gives \(a\).
- **Inequality Proofs:** Demonstrating that one side of an equation or inequality is consistently smaller or equal to another under defined conditions.
This problem can involve exploring algebraic manipulations or properties of inequalities to establish the stated relation. Additionally, one may need to consider the properties of metric spaces and the triangle inequality if dealing with potential complex formulations.
Expert Solution
Step 1
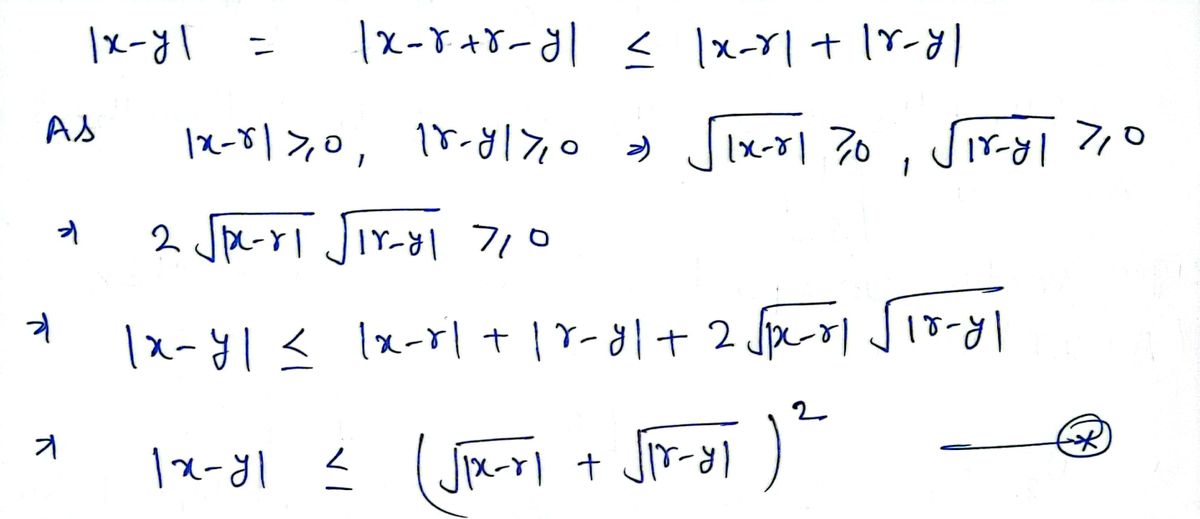
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

