Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![**Prove the identity.**
\[
\sin(x - \pi) = -\sin(x)
\]
Use the Subtraction Formula for Sine, and then simplify.
\[
\sin(x - \pi) = (\sin(x) \cdot \underline{\hspace{2em}}) - (\cos(x) \cdot \sin(\pi))
\]
\[
= (\sin(x) \cdot \underline{\hspace{2em}}) - (\cos(x) \cdot 0)
\]
\[
= \underline{\hspace{2em}}
\]
**Explanation of Solution Steps:**
To prove the identity \(\sin(x - \pi) = -\sin(x)\), we use the subtraction formula for sine:
1. The subtraction formula is:
\[
\sin(x - y) = \sin(x)\cos(y) - \cos(x)\sin(y)
\]
2. Plugging \(y = \pi\) into the formula:
\[
\sin(x - \pi) = \sin(x)\cos(\pi) - \cos(x)\sin(\pi)
\]
3. We know:
\(\cos(\pi) = -1\) and \(\sin(\pi) = 0\).
4. Substitute these values into the formula:
\[
\sin(x - \pi) = \sin(x)(-1) - \cos(x)(0)
\]
5. Simplify:
\[
= -\sin(x) + 0
= -\sin(x)
\]
Thus, the identity is proven.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F90e413d6-0f95-45bc-9120-3de888a1b336%2Fed0ae9c2-3741-40b2-8577-f9ea8c28447c%2Flcqo1us_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Prove the identity.**
\[
\sin(x - \pi) = -\sin(x)
\]
Use the Subtraction Formula for Sine, and then simplify.
\[
\sin(x - \pi) = (\sin(x) \cdot \underline{\hspace{2em}}) - (\cos(x) \cdot \sin(\pi))
\]
\[
= (\sin(x) \cdot \underline{\hspace{2em}}) - (\cos(x) \cdot 0)
\]
\[
= \underline{\hspace{2em}}
\]
**Explanation of Solution Steps:**
To prove the identity \(\sin(x - \pi) = -\sin(x)\), we use the subtraction formula for sine:
1. The subtraction formula is:
\[
\sin(x - y) = \sin(x)\cos(y) - \cos(x)\sin(y)
\]
2. Plugging \(y = \pi\) into the formula:
\[
\sin(x - \pi) = \sin(x)\cos(\pi) - \cos(x)\sin(\pi)
\]
3. We know:
\(\cos(\pi) = -1\) and \(\sin(\pi) = 0\).
4. Substitute these values into the formula:
\[
\sin(x - \pi) = \sin(x)(-1) - \cos(x)(0)
\]
5. Simplify:
\[
= -\sin(x) + 0
= -\sin(x)
\]
Thus, the identity is proven.
Expert Solution
Step 1
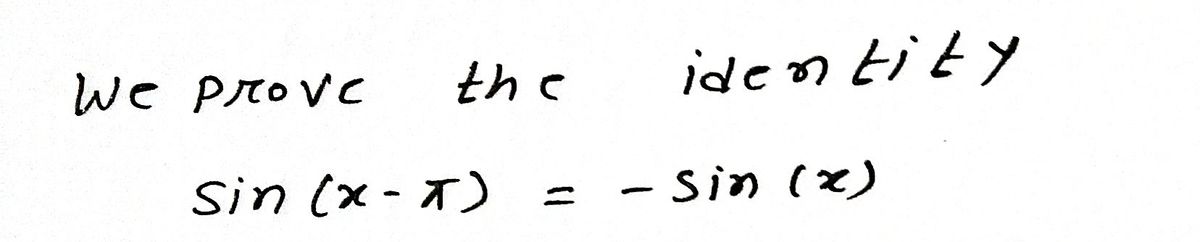
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning