Prove the identity. sec (-x) – sin(-x) tan(-x) = cosx
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
I need help with this. I've gotten a few steps so far but I cannot figure out the rest.
![## Prove the Identity
Given the trigonometric identity to prove:
\[ \sec(-x) - \sin(-x) \tan(-x) = \cos x \]
### Note
Each statement must be based on a rule chosen from the Rule menu. To see a detailed description of a rule, select the More Information Button to the right of the rule.
### Steps and Corresponding Rules
| Statement | Rule |
|------------------------------------------------|-----------|
| \(\sec(-x) - \sin(-x) \tan(-x)\) | |
| \(\sec(-x) - \sin(-x) \tan(-x)\) | Algebra |
| \(\sec x - \sin(-x) \tan(-x)\) | Odd/Even |
| \(\sec x - (-\sin x) \tan(-x)\) | Odd/Even |
| \(\sec x - (-\sin x) (-\tan x)\) | Odd/Even |
| \(\sec x - \sin x \tan x\) | Simplify |
| \(\boxed{\cos x}\) | Identity |
### Explanation of the Rules:
- **Algebra**: Simplifying the expression.
- **Odd/Even**: Applying properties of sine, cosine, and tangent for negative angles.
- **Simplify**: Reducing the expression to its simplest form.
- **Identity**: Using a fundamental trigonometric identity to conclude the proof.
### Diagram Explanation
To the right of the rule table, there is a selection menu which allows for the application of various trigonometric rules:
- The vertical scroll list includes different trigonometric rules and identities.
- Symbols such as \(\cos\), \(\sin\), \(\tan\), \(\cot\), \(\sec\), \(\csc\), \(\pi\), parentheses, and square roots allow for selecting specific trigonometric functions and constants.
- Additional buttons include a help icon (?), a reset button (↻), and a validation button (X).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F4c3dcdda-9290-4eb4-ba73-ee9de7b78657%2F097cd4fa-f40a-4567-afa7-0894084883a3%2Fv5efk76.png&w=3840&q=75)
Transcribed Image Text:## Prove the Identity
Given the trigonometric identity to prove:
\[ \sec(-x) - \sin(-x) \tan(-x) = \cos x \]
### Note
Each statement must be based on a rule chosen from the Rule menu. To see a detailed description of a rule, select the More Information Button to the right of the rule.
### Steps and Corresponding Rules
| Statement | Rule |
|------------------------------------------------|-----------|
| \(\sec(-x) - \sin(-x) \tan(-x)\) | |
| \(\sec(-x) - \sin(-x) \tan(-x)\) | Algebra |
| \(\sec x - \sin(-x) \tan(-x)\) | Odd/Even |
| \(\sec x - (-\sin x) \tan(-x)\) | Odd/Even |
| \(\sec x - (-\sin x) (-\tan x)\) | Odd/Even |
| \(\sec x - \sin x \tan x\) | Simplify |
| \(\boxed{\cos x}\) | Identity |
### Explanation of the Rules:
- **Algebra**: Simplifying the expression.
- **Odd/Even**: Applying properties of sine, cosine, and tangent for negative angles.
- **Simplify**: Reducing the expression to its simplest form.
- **Identity**: Using a fundamental trigonometric identity to conclude the proof.
### Diagram Explanation
To the right of the rule table, there is a selection menu which allows for the application of various trigonometric rules:
- The vertical scroll list includes different trigonometric rules and identities.
- Symbols such as \(\cos\), \(\sin\), \(\tan\), \(\cot\), \(\sec\), \(\csc\), \(\pi\), parentheses, and square roots allow for selecting specific trigonometric functions and constants.
- Additional buttons include a help icon (?), a reset button (↻), and a validation button (X).
Expert Solution
Step 1
Given,
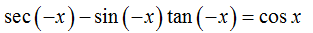
Step 2
Concept used:
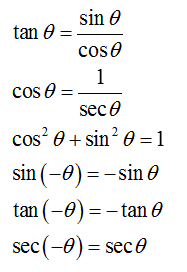
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning