Prove that Vn 2 2: 1++÷+ …+ 1 1 1 < 2 – ... 4 9 n2 n
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Topic Video
Question
Induction
![**Mathematical Proof Problem for Educational Purposes**
**Objective:** Prove that for all \( n \geq 2 \):
\[
1 + \frac{1}{4} + \frac{1}{9} + \cdots + \frac{1}{n^2} < 2 - \frac{1}{n}
\]
**Instructions:**
You are required to show the inequality holds by induction or any other suitable mathematical technique. Start by testing the base case, \( n = 2 \), and proceed with a logical argument to demonstrate that the expression is true for all integer values greater than or equal to 2.
**Note:** This problem involves understanding the summation of reciprocals of perfect squares and comparing it with a decreasing linear function. Consider representing terms with known inequalities or other mathematical series expansions if needed.
**Discussion and Examples:**
- Begin with known mathematical assertions or series comparisons.
- Think about how the series converges and its upper bound estimates.
- Utilize graphical representations or mathematical simulations, if possible, to illustrate the inequality visually.
This task is intended to strengthen problem-solving skills and understanding of series and inequalities.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2a4cecdd-94f1-45ae-b6d2-43e39cc00a4c%2Fa663bb94-8803-491f-9303-9a7ab56e974a%2Fak7zjg_processed.png&w=3840&q=75)
Transcribed Image Text:**Mathematical Proof Problem for Educational Purposes**
**Objective:** Prove that for all \( n \geq 2 \):
\[
1 + \frac{1}{4} + \frac{1}{9} + \cdots + \frac{1}{n^2} < 2 - \frac{1}{n}
\]
**Instructions:**
You are required to show the inequality holds by induction or any other suitable mathematical technique. Start by testing the base case, \( n = 2 \), and proceed with a logical argument to demonstrate that the expression is true for all integer values greater than or equal to 2.
**Note:** This problem involves understanding the summation of reciprocals of perfect squares and comparing it with a decreasing linear function. Consider representing terms with known inequalities or other mathematical series expansions if needed.
**Discussion and Examples:**
- Begin with known mathematical assertions or series comparisons.
- Think about how the series converges and its upper bound estimates.
- Utilize graphical representations or mathematical simulations, if possible, to illustrate the inequality visually.
This task is intended to strengthen problem-solving skills and understanding of series and inequalities.
Expert Solution
Step 1
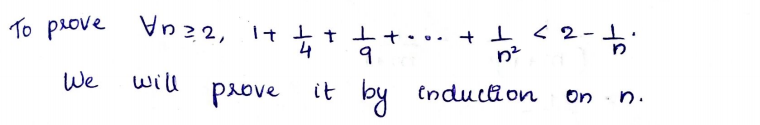
Step by step
Solved in 3 steps with 5 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

