Homework Help is Here – Start Your Trial Now!
Science
Advanced Physics
Problem 8. The Cosmic Microwave Background (CMB) acts as a perfect black body whose energy spectrum (energy density per unit volume per unit frequency) is given by the expression 8пh f³ e³ exp(hf/kT) -1° This expression gives the energy density in the frequency range f to f+df. 1. Find dimensions of the quantities (a) e and (b) hf/kT. (f)df = df. 2. The peak location of e(f) is such that hfpeak show that fpeak lies in the microwave¹ range. 3. To calculate the total energy density, integrate Eq. (4.1) over the whole frequency range and show that 6₁ (T) = e(tas = 77²k4 15h³3 7ª, using (4.2) 4. Express Eq. (4.1) in terms of wavelength A. (4.1) 2.82kT. Assuming present CMB temperature is 2.73 K, r³dr 1 e

Problem 8. The Cosmic Microwave Background (CMB) acts as a perfect black body whose energy spectrum (energy density per unit volume per unit frequency) is given by the expression 8пh f³ e³ exp(hf/kT) -1° This expression gives the energy density in the frequency range f to f+df. 1. Find dimensions of the quantities (a) e and (b) hf/kT. (f)df = df. 2. The peak location of e(f) is such that hfpeak show that fpeak lies in the microwave¹ range. 3. To calculate the total energy density, integrate Eq. (4.1) over the whole frequency range and show that 6₁ (T) = e(tas = 77²k4 15h³3 7ª, using (4.2) 4. Express Eq. (4.1) in terms of wavelength A. (4.1) 2.82kT. Assuming present CMB temperature is 2.73 K, r³dr 1 e

icon
Related questions
Question
100%

 Cosmic Microwave Background

8. The Cosmic Microwave Background (CMB) acts as a perfect black body whose energy spectrum
(energy density per unit volume per unit frequency) is given by the expression : (image attached)

Problem 8. The Cosmic Microwave Background (CMB) acts as a perfect black body whose energy spectrum (energy density per unit volume per unit frequency) is given by the expression (f)df = 8Th c³ exp(hf/KT)-1df. This expression gives the energy density in the frequency range f to f+df. 1. Find dimensions of the quantities (a) and (b) hf/kT. E₁ (T) = 2. The peak location of e(f) is such that hfpeak≈ 2.82kT. Assuming present CMB temperature is 2.73 K, show that fpeak lies in the microwave¹ range. 3. To calculate the total energy density, integrate Eq. (4.1) over the whole frequency range and show that π²k4 2³ dr ")==(f)df = 15³37², using T, Sº (4.2) 4. Express Eq. (4.1) in terms of wavelength A. ex (4.1) 774 15
Transcribed Image Text:Problem 8. The Cosmic Microwave Background (CMB) acts as a perfect black body whose energy spectrum (energy density per unit volume per unit frequency) is given by the expression (f)df = 8Th c³ exp(hf/KT)-1df. This expression gives the energy density in the frequency range f to f+df. 1. Find dimensions of the quantities (a) and (b) hf/kT. E₁ (T) = 2. The peak location of e(f) is such that hfpeak≈ 2.82kT. Assuming present CMB temperature is 2.73 K, show that fpeak lies in the microwave¹ range. 3. To calculate the total energy density, integrate Eq. (4.1) over the whole frequency range and show that π²k4 2³ dr ")==(f)df = 15³37², using T, Sº (4.2) 4. Express Eq. (4.1) in terms of wavelength A. ex (4.1) 774 15
Expert Solution
Part 1

θ is the dimension of temperature

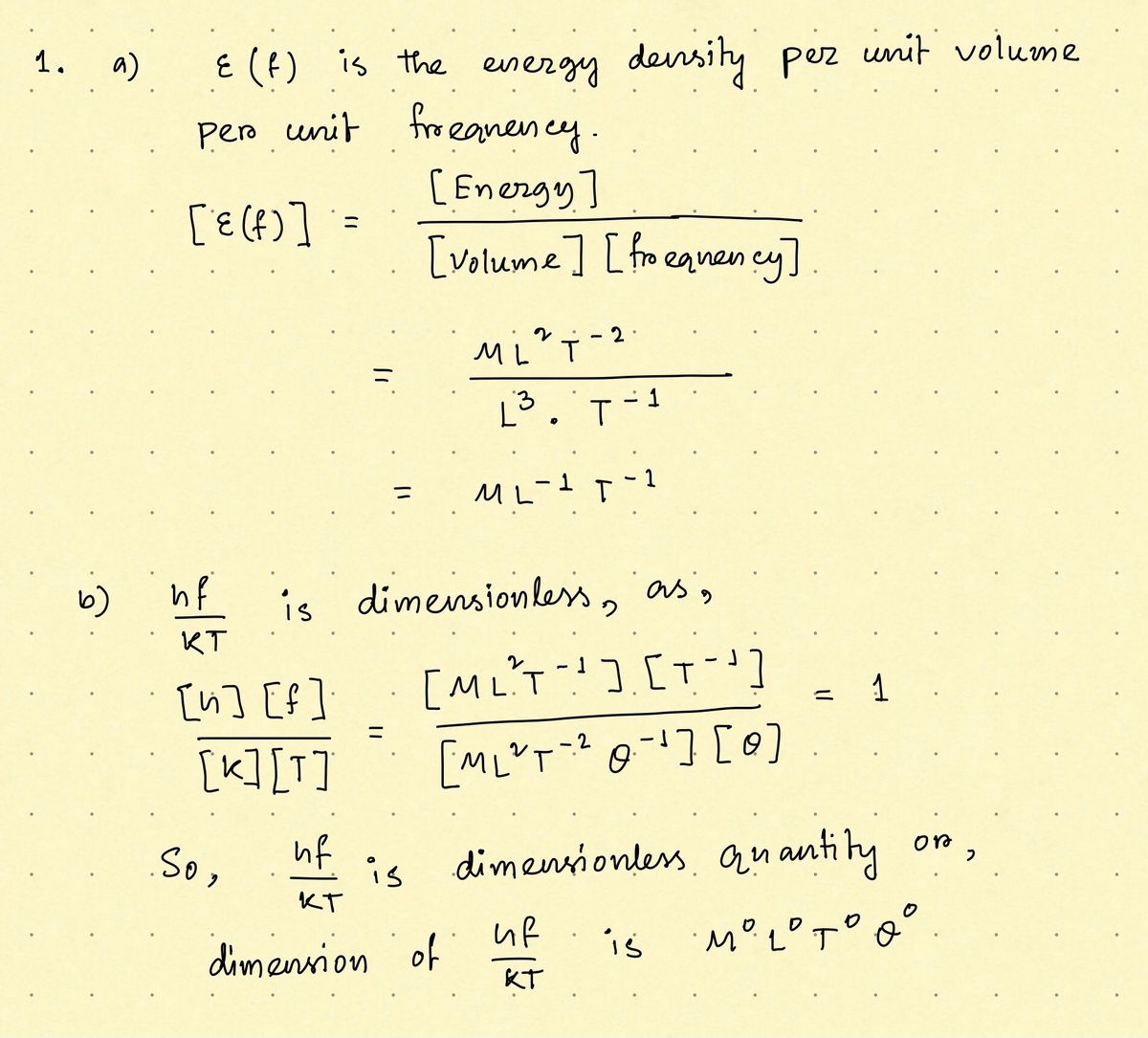
Advanced Physics homework question answer, step 1, image 1

steps

Step by step

Solved in 4 steps with 4 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer