Problem 7.1.14. (a) Provide a rigorous definition for lim sn # s. (b) Use your definition to show that for any real number a, lim ((-1)")+ a. Hint. Choose ɛ = 1 and use the fact that a - (-1)" < 1 is equivalent to (-1)" – 1 < a < (-1)" +1 to show that no choice of N will work for this ɛ.
Problem 7.1.14. (a) Provide a rigorous definition for lim sn # s. (b) Use your definition to show that for any real number a, lim ((-1)")+ a. Hint. Choose ɛ = 1 and use the fact that a - (-1)" < 1 is equivalent to (-1)" – 1 < a < (-1)" +1 to show that no choice of N will work for this ɛ.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%
Please help me solve problem 7.1.14

Transcribed Image Text:11:09 O
our intuition was, in fact, correct and do
so in a very prescribed manner. For
example, if b > 0 is a fixed number, then
you would probably say as n approaches
infinity, b() approaches 6º = 1. After all,
we did already prove that lim,,→, = 0.
We should be able to back up this intuition
with our rigorous definition.
Problem 7.1.13. Let b > 0. Use the
definition to prove lim b)
1.
Hint. You will probably need to
separate this into two cases: 0 < b < 1
and b > 1.
Problem 7.1.14.
(a) Provide a rigorous definition for
lim sn + s.
(b) Use your definition to show that for
any real number a, lim ((-1)")+ a.
Hint. Choose e = 1 and use the fact
that a – (-1)"| < 1 is equivalent to
(-1)" – 1 < a < (-1)" +1 to show that
no choice of N will work for this ɛ.
II
II
Expert Solution
Step 1
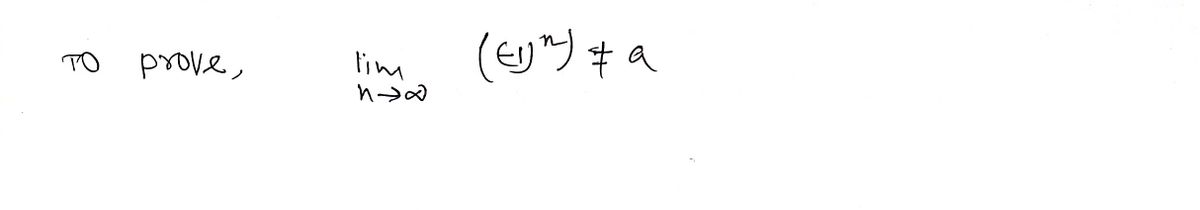
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

