Problem 6. Explain why the coefficient of x'y the same as the coefficient of x'y in the expansion of (x+y)"?
Problem 6. Explain why the coefficient of x'y the same as the coefficient of x'y in the expansion of (x+y)"?
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Problem 6.**
Explain why the coefficient of \(x^5y^3\) is the same as the coefficient of \(x^3y^5\) in the expansion of \((x+y)^8\)?
**Explanation:**
In the binomial expansion of \((x+y)^n\), the general term is given by:
\[
\binom{n}{k} x^{n-k}y^k
\]
For the given expansion \((x+y)^8\), we look at two specific terms: \(x^5y^3\) and \(x^3y^5\).
1. **Coefficient of \(x^5y^3\):**
Applying the binomial formula, the coefficient is:
\[
\binom{8}{3} = \frac{8 \times 7 \times 6}{3 \times 2 \times 1} = 56
\]
2. **Coefficient of \(x^3y^5\):**
Similarly, using the binomial formula, the coefficient is:
\[
\binom{8}{5} = \frac{8 \times 7 \times 6}{3 \times 2 \times 1} = 56
\]
**Conclusion:**
The coefficients are the same because of the symmetry property of binomial coefficients, where \(\binom{n}{k} = \binom{n}{n-k}\). In this case, \(\binom{8}{3} = \binom{8}{5}\), showing that the coefficients of \(x^5y^3\) and \(x^3y^5\) are indeed equal. This symmetry arises from the fact that switching the roles of \(x\) and \(y\) does not change the overall expansion equation.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F6f77c388-8d90-48d1-91c3-9cd900e6ca37%2Fb3f145a9-f2f2-42c3-b477-1644e224e901%2F1zrn09_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem 6.**
Explain why the coefficient of \(x^5y^3\) is the same as the coefficient of \(x^3y^5\) in the expansion of \((x+y)^8\)?
**Explanation:**
In the binomial expansion of \((x+y)^n\), the general term is given by:
\[
\binom{n}{k} x^{n-k}y^k
\]
For the given expansion \((x+y)^8\), we look at two specific terms: \(x^5y^3\) and \(x^3y^5\).
1. **Coefficient of \(x^5y^3\):**
Applying the binomial formula, the coefficient is:
\[
\binom{8}{3} = \frac{8 \times 7 \times 6}{3 \times 2 \times 1} = 56
\]
2. **Coefficient of \(x^3y^5\):**
Similarly, using the binomial formula, the coefficient is:
\[
\binom{8}{5} = \frac{8 \times 7 \times 6}{3 \times 2 \times 1} = 56
\]
**Conclusion:**
The coefficients are the same because of the symmetry property of binomial coefficients, where \(\binom{n}{k} = \binom{n}{n-k}\). In this case, \(\binom{8}{3} = \binom{8}{5}\), showing that the coefficients of \(x^5y^3\) and \(x^3y^5\) are indeed equal. This symmetry arises from the fact that switching the roles of \(x\) and \(y\) does not change the overall expansion equation.
Expert Solution
Step 1
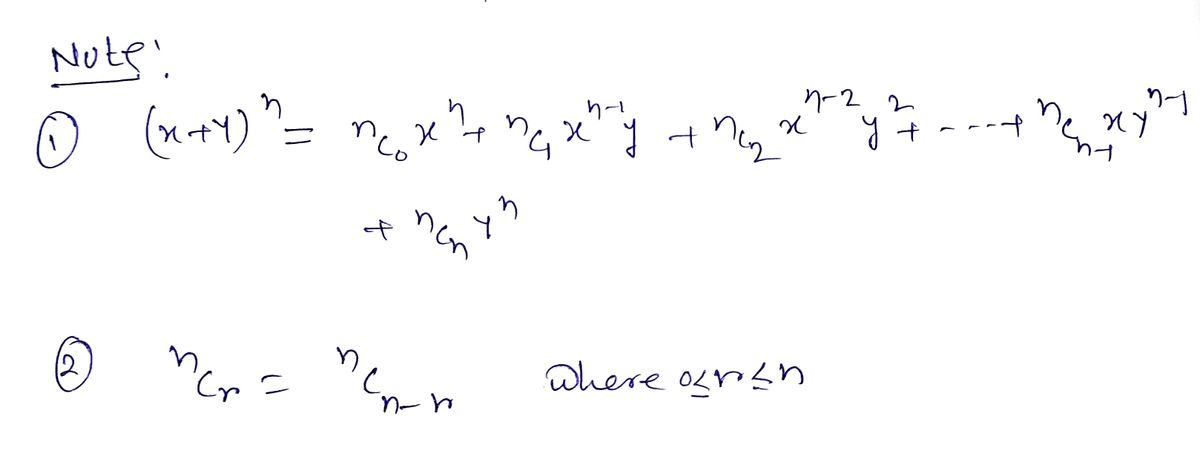
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

