Discrete Mathematics 7 of 10PROBLEM 6Part 1. Give the adjacency matrix for the graph G as pictured helow:Figure 2: A gruph shous 6 vertices and 9 edges. The vertices are 1, 2, 3, 4,5. and 6, repnsented by circles. The edges between the rertices are epresented byarruus, as follous: 4 to 3: 3 to 2; 2 to 1: 1 to 6: 6 to 2; 3 to 4: 4 to 5; 5 to 6; anda self loop on zerter 5.Part 2. A directed graph G has 5 vertices, numbered 1 through 5. The 5 x 5matrix A is the adjacency matrix for G. The matrices A and A are given below.0100 00 0 1 0 01000 0100 1 001101A =1000 001A =0010001 10 11.1010Use the information given to answer the questions about the graph G.fa) Which vertices can reach vertex 2 by a walk of length 3?(b) Is there a walk of length 4 from vertex 4 to vertex 5 in G? (Hint: A =A A.)

To find- Part A. Give the adjacency matrix for the graph G as pictured below.…

Answered: PROBLEM 6 Part 1. Give the adjacency…

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

Related questions

Question

Discrete Mathematics

Expert Solution

Step 1

To find-

Part A. Give the adjacency matrix for the graph G as pictured below.
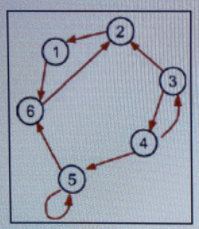
Part B. A directed graph G has 5 vertices, numbered 1 through 5. The $5 \times 5$ matrix A is the adjacency matrix of G. The matrices $A^{2}$ and $A^{3}$ are given below: $A^{2} = (\begin{matrix} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 1 \end{matrix}), A^{3} = (\begin{matrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 \end{matrix})$ .