Problem 4 (Non-homogeneous Equations Redux). By now we are very procedure for solving a linear, second-order initial value problem y" + p(t)y' + q(t)y = f(t), y(to) = y0, y'(to) = vo- %3D • First find the general solution to the associated homogeneous equati- y" + p(t)y/ + q(t)y = 0. %3D • Find a particular solution to the non-homogeneous equation y" + p(t)y' + q(t)y = f(t) %3D and add it to the homogeneous solution. • Plug in the initial conditions to find the solution to the IVP. There is actually another way we can proceed, and it allows us to plug the into the homogeneous solution before finding the particular solution. (a) Suppose u1(t) is a solution to the initial value problem y" + p(t)y' + q(t)y = 0, y(to) = yo, y (to) = %3D %3D and u2(t) is a solution to y" + p(t)y' + q(t)y = f(t), y(to) = 0, y (to) = 0. %3D %3D %3D Show that y(t) = u1 (t) + u2 (t) is a solution to the original initial val %3D
Problem 4 (Non-homogeneous Equations Redux). By now we are very procedure for solving a linear, second-order initial value problem y" + p(t)y' + q(t)y = f(t), y(to) = y0, y'(to) = vo- %3D • First find the general solution to the associated homogeneous equati- y" + p(t)y/ + q(t)y = 0. %3D • Find a particular solution to the non-homogeneous equation y" + p(t)y' + q(t)y = f(t) %3D and add it to the homogeneous solution. • Plug in the initial conditions to find the solution to the IVP. There is actually another way we can proceed, and it allows us to plug the into the homogeneous solution before finding the particular solution. (a) Suppose u1(t) is a solution to the initial value problem y" + p(t)y' + q(t)y = 0, y(to) = yo, y (to) = %3D %3D and u2(t) is a solution to y" + p(t)y' + q(t)y = f(t), y(to) = 0, y (to) = 0. %3D %3D %3D Show that y(t) = u1 (t) + u2 (t) is a solution to the original initial val %3D
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Transcribed Image Text:Problem 4 (Non-homogeneous Equations Redux). By now we are very
procedure for solving a linear, second-order initial value problem
y" + p(t)y' + q(t)y = f(t), y(to) = y0, y'(to) = vo-
%3D
• First find the general solution to the associated homogeneous equati-
y" + p(t)y/ + q(t)y = 0.
%3D
• Find a particular solution to the non-homogeneous equation
y" + p(t)y' + q(t)y = f(t)
%3D
and add it to the homogeneous solution.
• Plug in the initial conditions to find the solution to the IVP.
There is actually another way we can proceed, and it allows us to plug the
into the homogeneous solution before finding the particular solution.
(a) Suppose u1(t) is a solution to the initial value problem
y" + p(t)y' + q(t)y = 0, y(to) = yo, y (to) =
%3D
%3D
and u2(t) is a solution to
y" + p(t)y' + q(t)y = f(t), y(to) = 0, y (to) = 0.
%3D
%3D
%3D
Show that y(t) = u1 (t) + u2 (t) is a solution to the original initial val
%3D
Expert Solution
Step 1
NOTE: According to guideline answer of first question can be given, for other please ask in a different question and specify the question number .
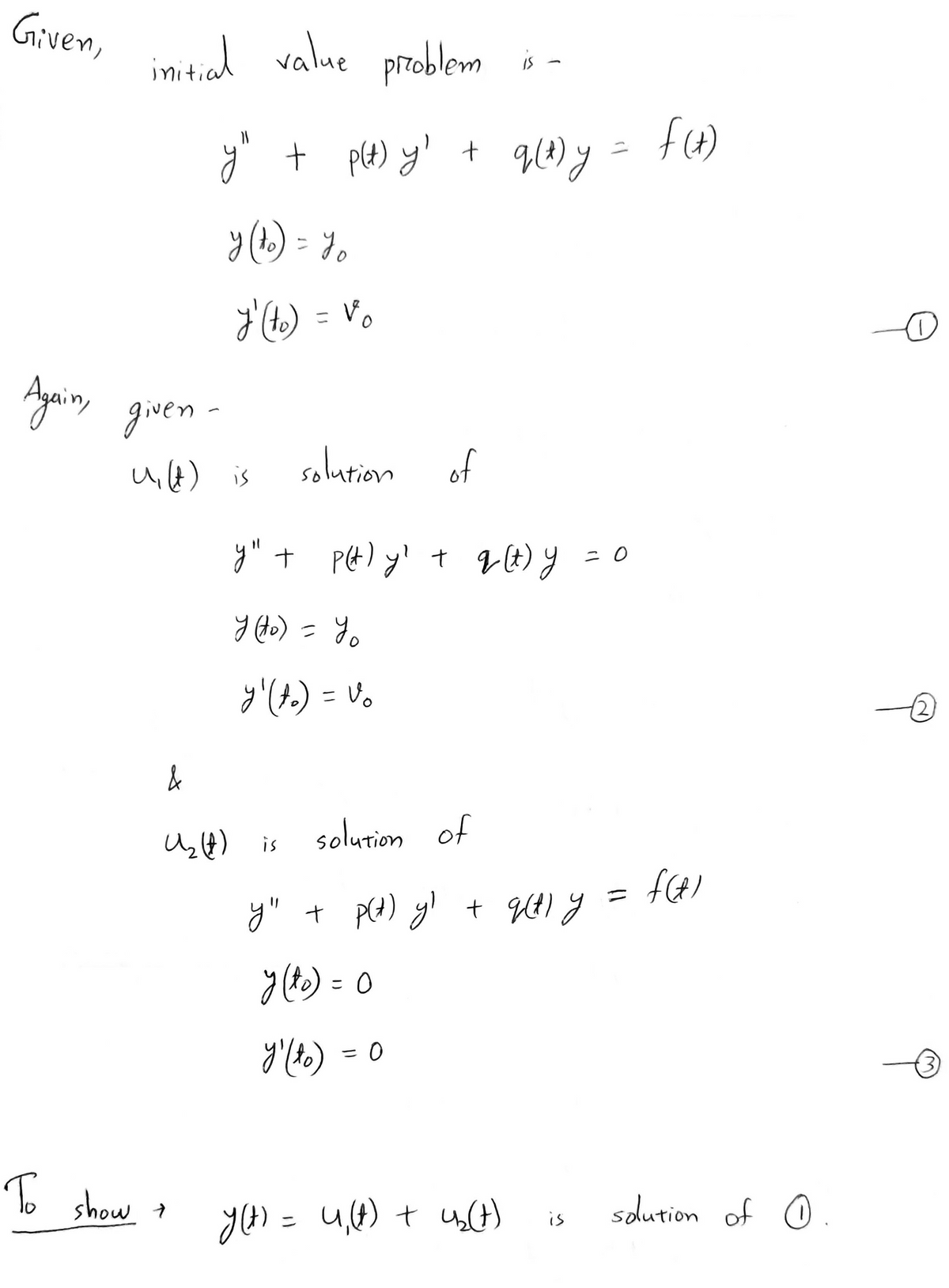
Step by step
Solved in 2 steps with 3 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
