Problem 3. The purpose of this problem is to get you to work though an actual Diffie-Hellman ephemeral key exchange algorithm. (The algorithm itself can be found in the slides for the Video "Intro to Public Key Crypto".) Recall that the parties have to agree in advance on a generator g and a prime modulus p. For all parts of this problem, g = 513 and p = 65537. Note that these are small enough numbers that you can do the computation in most programming languages with 64-bit (unsigned) integers, as long as you always multiply by g and then reduce mod p before multiplying again (rather than exponentiating all at once). Also, the command-line tools de and be can handle arbitrarily large integers, so you can do the exponentiation all at once. a. You want to establish a shared key with Bob using Diffie-Hellman algorithm (unauthenticated assume you will authenticate each other using some other mechanism later). Pick a random private number between 1 and 65536 inclusive. What is your number, and what is the "public number" that you send Bob? b. Bob sends you his public number: 52242. What is the resulting secret (number) that you and Bob end up sharing? c. For this part you must break Diffie-Hellman, to emphasize the need to use much larger numbers for and a than we are using here.
Problem 3. The purpose of this problem is to get you to work though an actual Diffie-Hellman ephemeral key exchange algorithm. (The algorithm itself can be found in the slides for the Video "Intro to Public Key Crypto".) Recall that the parties have to agree in advance on a generator g and a prime modulus p. For all parts of this problem, g = 513 and p = 65537. Note that these are small enough numbers that you can do the computation in most programming languages with 64-bit (unsigned) integers, as long as you always multiply by g and then reduce mod p before multiplying again (rather than exponentiating all at once). Also, the command-line tools de and be can handle arbitrarily large integers, so you can do the exponentiation all at once. a. You want to establish a shared key with Bob using Diffie-Hellman algorithm (unauthenticated assume you will authenticate each other using some other mechanism later). Pick a random private number between 1 and 65536 inclusive. What is your number, and what is the "public number" that you send Bob? b. Bob sends you his public number: 52242. What is the resulting secret (number) that you and Bob end up sharing? c. For this part you must break Diffie-Hellman, to emphasize the need to use much larger numbers for and a than we are using here.
Database System Concepts
7th Edition
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Chapter1: Introduction
Section: Chapter Questions
Problem 1PE
Related questions
Question
100%

Transcribed Image Text:Problem 3. The purpose of this problem is to get you to work though an actual Diffie-Hellman
ephemeral key exchange algorithm. (The algorithm itself can be found in the slides for the Video
"Intro to Public Key Crypto".)
Recall that the parties have to agree in advance on a generator g and a prime modulus p. For all
parts of this problem, g = 513 and p = 65537. Note that these are small enough numbers that
you can do the computation in most programming languages with 64-bit (unsigned) integers, as
long as you always multiply by g and then reduce mod p before multiplying again (rather than
exponentiating all at once). Also, the command-line tools de and be can handle arbitrarily large
integers, so you can do the exponentiation all at once.
a. You want to establish a shared key with Bob using Diffie-Hellman algorithm (unauthenticated
assume you will authenticate each other using some other mechanism later). Pick a random
private number between 1 and 65536 inclusive. What is your number, and what is the "public
number" that you send Bob?
b. Bob sends you his public number: 52242. What is the resulting secret (number) that you and
Bob end up sharing?
c. For this part you must break Diffie-Hellman, to emphasize the need to use much larger numbers
for p and g than we are using here.
Suppose you eavesdropped on a conversation between Alice and Charlie, who used Diffic
Hellman with the same parameters as above. You observed that Alice's public number is
43080 and Charlie's is 31330. What is the secret key that they derived? (In other words: solve
the discrete log problem to get Alice and Charlie's private numbers, and then run the DH
algorithm to get the secret key. You will have to use brute force, i.e., try all the possibilities
until you find one of the discrete logs, but the program is trivial a while loop with a 2-line
1
body and it takes very little time on a modern computer. Java has a BigInteger class with a
built-in modExp() method, and other languages may also.)
Expert Solution
Step 1
Answer :-
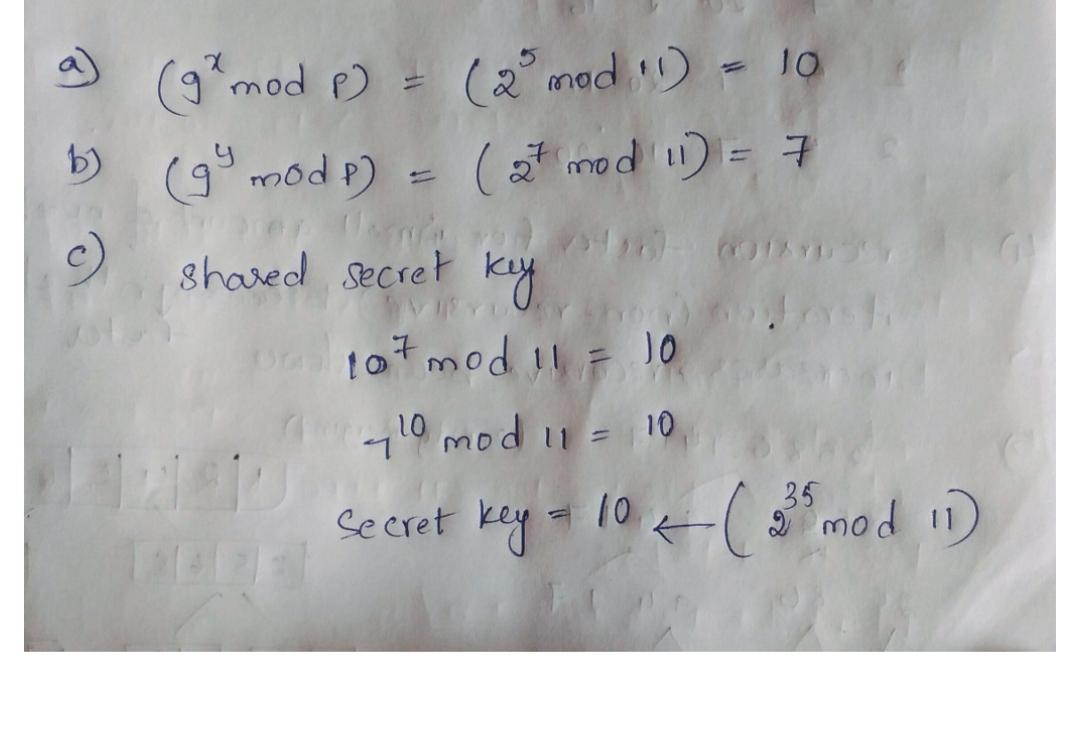
Step by step
Solved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Recommended textbooks for you

Database System Concepts
Computer Science
ISBN:
9780078022159
Author:
Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:
McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:
9780134444321
Author:
Tony Gaddis
Publisher:
PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:
9780132737968
Author:
Thomas L. Floyd
Publisher:
PEARSON

Database System Concepts
Computer Science
ISBN:
9780078022159
Author:
Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:
McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:
9780134444321
Author:
Tony Gaddis
Publisher:
PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:
9780132737968
Author:
Thomas L. Floyd
Publisher:
PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:
9780133976892
Author:
Paul J. Deitel, Harvey Deitel
Publisher:
PEARSON

Database Systems: Design, Implementation, & Manag…
Computer Science
ISBN:
9781337627900
Author:
Carlos Coronel, Steven Morris
Publisher:
Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education