Problem 1: A 5.7-m ladder rests against a wall as shown. The ladder has a mass of 26.3 kg. A 58.3-kg person stands on the ladder at a distance of 3.6 m from the bottom of the ladder. The foot of the ladder is 1.5 m from the bottom the wall. Assume there is no friction between the ladder and the wall so that the force of the wall on the ladder is acting only in the horizontal direction. However, there is a friction force between the ladder and the ground. ladder Part (a) What is the force, in N, exerted by the wall on the ladder? Numeric : Anumeric value is expected and not an expression. Fw Part (b) What is the normal force, in N, exerted by the floor on the ladder? Numeric : A numeric value is expected and not an expression. Fy = Part (c) What is the friction force, in N, between the ladder and the ground? Numeric : Anumeric value is expected and not an expression. Ff=
Rotational Equilibrium And Rotational Dynamics
In physics, the state of balance between the forces and the dynamics of motion is called the equilibrium state. The balance between various forces acting on a system in a rotational motion is called rotational equilibrium or rotational dynamics.
Equilibrium of Forces
The tension created on one body during push or pull is known as force.

Consider the following diagram which represents all the forces involved.
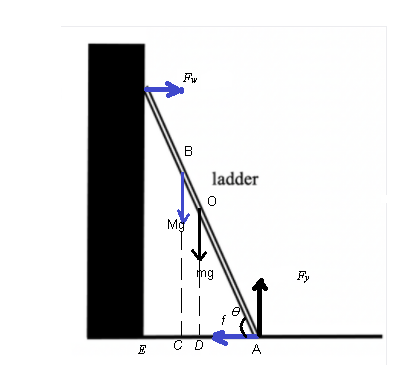
Let Fw be the normal reaction force exerted on the ladder by the wall, Fy is the normal reaction force exerted on the ladder by the floor, Ff is the force of friction between the ladder and the ground, Mg is the weight of the person, the distance of the foot of the ladder from the bottom of the wall be R, and mg is the weight of the ladder.
Note:
The weight of the ladder acts at the center of the ladder O.
Let the length of the ladder be L, the angle made by the ladder from the ground be Ө, and the distance of the position of the person from the bottom be x.
AO = L/2
AB = 3.6 m
AE = 1.5 m
In equilibrium, the net force acting on the ladder and the net torque of all the forces acting on the ladder about A both would be equal to zero.
a)
On applying the equilibrium condition, the net torque due to all the forces about the pivot A would be equal to zero.
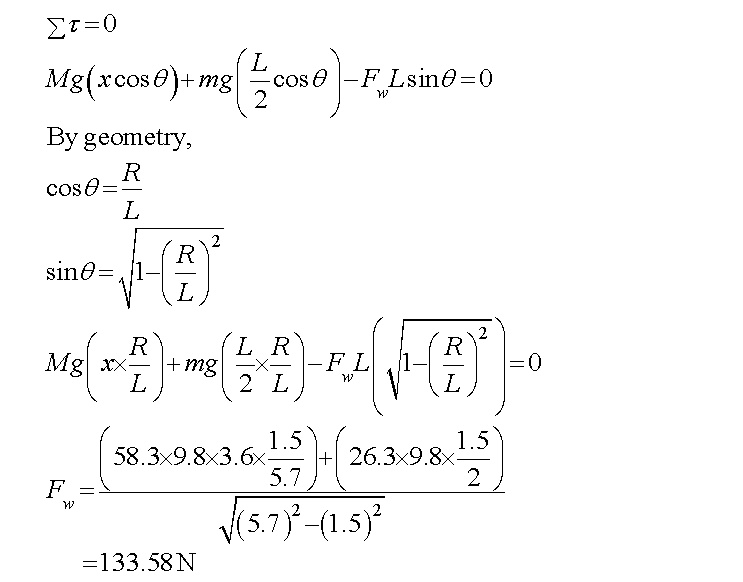
Step by step
Solved in 2 steps with 4 images









