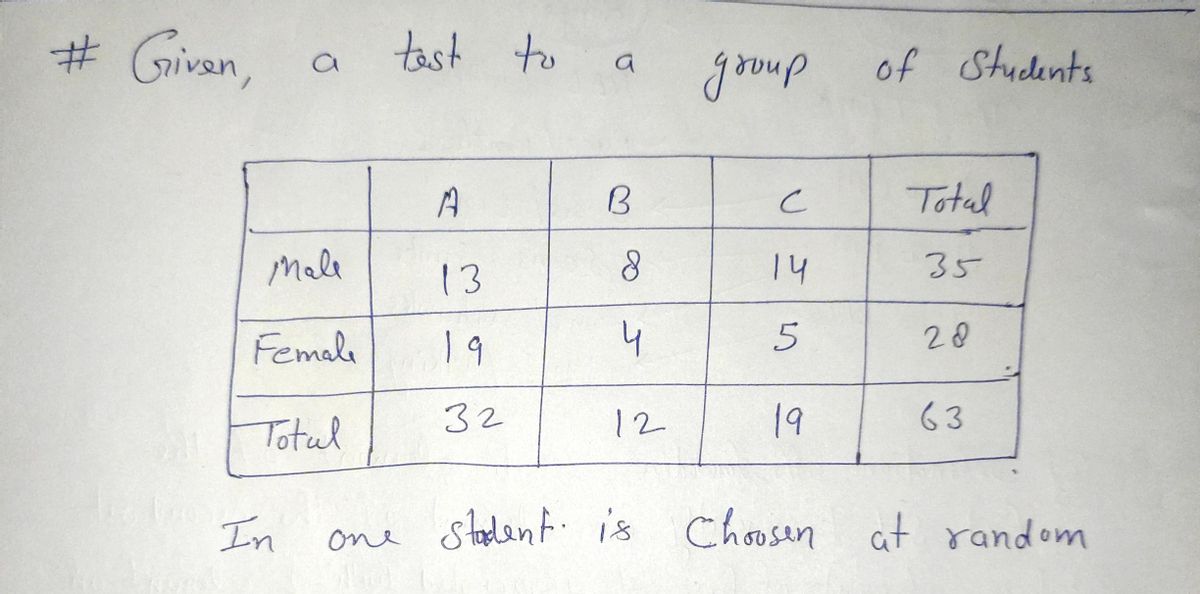
### Probability and Statistics: Understanding Probability with a Venn Diagram Approach **Scenario:** A test is administered to a group of students, and the results are summarized by gender and grade in the table below. **Table: Summary of Grades by Gender** | | A | B | C | Total | |----------|----|----|----|-------| | Male | 13 | 8 | 14 | 35 | | Female | 19 | 4 | 5 | 28 | | **Total**| 32 | 12 | 19 | 63 | **Problem:** If one student is chosen at random, find the probability that the student was male OR got an “A”. **Solution:** To solve this probability problem, we can use the concept of the union of two events: being male or receiving an "A." 1. **Calculate Individual Probabilities:** - Probability of a student being male: \( P(\text{Male}) = \frac{35}{63} \) - Probability of a student getting an "A": \( P(A) = \frac{32}{63} \) 2. **Calculate the Probability of Both Events Happening:** - Probability of being a male who got an "A": \( P(\text{Male and A}) = \frac{13}{63} \) 3. **Apply the Formula for Union of Two Probabilities:** \[ P(\text{Male OR A}) = P(\text{Male}) + P(A) - P(\text{Male and A}) \] 4. **Substitute the Values:** \[ P(\text{Male OR A}) = \frac{35}{63} + \frac{32}{63} - \frac{13}{63} = \frac{54}{63} \] 5. **Simplify the Probability:** \[ P(\text{Male OR A}) = \frac{6}{7} \] Thus, the probability that a randomly chosen student is either male or received an "A" is \(\frac{6}{7}\). **Interactive Component:** - View a step-by-step video explaining how to use Venn diagrams to visualize this probability problem. - Practice further by submitting your answer to ensure understanding. [Submit Question] ### Conclusion:
### Probability and Statistics: Understanding Probability with a Venn Diagram Approach **Scenario:** A test is administered to a group of students, and the results are summarized by gender and grade in the table below. **Table: Summary of Grades by Gender** | | A | B | C | Total | |----------|----|----|----|-------| | Male | 13 | 8 | 14 | 35 | | Female | 19 | 4 | 5 | 28 | | **Total**| 32 | 12 | 19 | 63 | **Problem:** If one student is chosen at random, find the probability that the student was male OR got an “A”. **Solution:** To solve this probability problem, we can use the concept of the union of two events: being male or receiving an "A." 1. **Calculate Individual Probabilities:** - Probability of a student being male: \( P(\text{Male}) = \frac{35}{63} \) - Probability of a student getting an "A": \( P(A) = \frac{32}{63} \) 2. **Calculate the Probability of Both Events Happening:** - Probability of being a male who got an "A": \( P(\text{Male and A}) = \frac{13}{63} \) 3. **Apply the Formula for Union of Two Probabilities:** \[ P(\text{Male OR A}) = P(\text{Male}) + P(A) - P(\text{Male and A}) \] 4. **Substitute the Values:** \[ P(\text{Male OR A}) = \frac{35}{63} + \frac{32}{63} - \frac{13}{63} = \frac{54}{63} \] 5. **Simplify the Probability:** \[ P(\text{Male OR A}) = \frac{6}{7} \] Thus, the probability that a randomly chosen student is either male or received an "A" is \(\frac{6}{7}\). **Interactive Component:** - View a step-by-step video explaining how to use Venn diagrams to visualize this probability problem. - Practice further by submitting your answer to ensure understanding. [Submit Question] ### Conclusion:
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
![### Probability and Statistics: Understanding Probability with a Venn Diagram Approach
**Scenario:**
A test is administered to a group of students, and the results are summarized by gender and grade in the table below.
**Table: Summary of Grades by Gender**
| | A | B | C | Total |
|----------|----|----|----|-------|
| Male | 13 | 8 | 14 | 35 |
| Female | 19 | 4 | 5 | 28 |
| **Total**| 32 | 12 | 19 | 63 |
**Problem:**
If one student is chosen at random, find the probability that the student was male OR got an “A”.
**Solution:**
To solve this probability problem, we can use the concept of the union of two events: being male or receiving an "A."
1. **Calculate Individual Probabilities:**
- Probability of a student being male: \( P(\text{Male}) = \frac{35}{63} \)
- Probability of a student getting an "A": \( P(A) = \frac{32}{63} \)
2. **Calculate the Probability of Both Events Happening:**
- Probability of being a male who got an "A": \( P(\text{Male and A}) = \frac{13}{63} \)
3. **Apply the Formula for Union of Two Probabilities:**
\[
P(\text{Male OR A}) = P(\text{Male}) + P(A) - P(\text{Male and A})
\]
4. **Substitute the Values:**
\[
P(\text{Male OR A}) = \frac{35}{63} + \frac{32}{63} - \frac{13}{63} = \frac{54}{63}
\]
5. **Simplify the Probability:**
\[
P(\text{Male OR A}) = \frac{6}{7}
\]
Thus, the probability that a randomly chosen student is either male or received an "A" is \(\frac{6}{7}\).
**Interactive Component:**
- View a step-by-step video explaining how to use Venn diagrams to visualize this probability problem.
- Practice further by submitting your answer to ensure understanding.
[Submit Question]
### Conclusion:](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F33614614-cd9e-4559-9a21-56f7eb77d3ea%2Fc32d9cef-7df7-49fb-b6c6-9bb6576f49a4%2F8k5avfl.jpeg&w=3840&q=75)
Transcribed Image Text:### Probability and Statistics: Understanding Probability with a Venn Diagram Approach
**Scenario:**
A test is administered to a group of students, and the results are summarized by gender and grade in the table below.
**Table: Summary of Grades by Gender**
| | A | B | C | Total |
|----------|----|----|----|-------|
| Male | 13 | 8 | 14 | 35 |
| Female | 19 | 4 | 5 | 28 |
| **Total**| 32 | 12 | 19 | 63 |
**Problem:**
If one student is chosen at random, find the probability that the student was male OR got an “A”.
**Solution:**
To solve this probability problem, we can use the concept of the union of two events: being male or receiving an "A."
1. **Calculate Individual Probabilities:**
- Probability of a student being male: \( P(\text{Male}) = \frac{35}{63} \)
- Probability of a student getting an "A": \( P(A) = \frac{32}{63} \)
2. **Calculate the Probability of Both Events Happening:**
- Probability of being a male who got an "A": \( P(\text{Male and A}) = \frac{13}{63} \)
3. **Apply the Formula for Union of Two Probabilities:**
\[
P(\text{Male OR A}) = P(\text{Male}) + P(A) - P(\text{Male and A})
\]
4. **Substitute the Values:**
\[
P(\text{Male OR A}) = \frac{35}{63} + \frac{32}{63} - \frac{13}{63} = \frac{54}{63}
\]
5. **Simplify the Probability:**
\[
P(\text{Male OR A}) = \frac{6}{7}
\]
Thus, the probability that a randomly chosen student is either male or received an "A" is \(\frac{6}{7}\).
**Interactive Component:**
- View a step-by-step video explaining how to use Venn diagrams to visualize this probability problem.
- Practice further by submitting your answer to ensure understanding.
[Submit Question]
### Conclusion:
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
