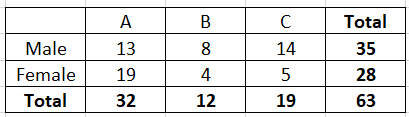
**Probability of Selecting a Male Student or a Student with an "A" Grade** In this probability exercise, we analyze a group of students based on their grades and gender. The following table summarizes the distribution: | | A | B | C | Total | |--------|----|----|----|-------| | Male | 13 | 8 | 14 | 35 | | Female | 19 | 4 | 5 | 28 | | Total | 32 | 12 | 19 | 63 | **Objective:** Determine the probability that a randomly selected student is either male or has received an "A" grade. To solve this, we need to calculate: 1. Total students who are male. 2. Total students who received an "A". 3. Use the formula for probability with "or" condition: \[ P(\text{Male or A}) = P(\text{Male}) + P(\text{A}) - P(\text{Male and A}) \] - **Total students**: 63 - **Total males**: 35 - **Total students with an "A"**: 32 - **Males with an "A"**: 13 Using the formula: \[ P(\text{Male or A}) = \frac{35}{63} + \frac{32}{63} - \frac{13}{63} = \frac{54}{63} = \frac{18}{21} \approx 0.857 \] **Conclusion:** The probability that a randomly selected student is either male or received an "A" is approximately 0.857, or 85.7%.
**Probability of Selecting a Male Student or a Student with an "A" Grade** In this probability exercise, we analyze a group of students based on their grades and gender. The following table summarizes the distribution: | | A | B | C | Total | |--------|----|----|----|-------| | Male | 13 | 8 | 14 | 35 | | Female | 19 | 4 | 5 | 28 | | Total | 32 | 12 | 19 | 63 | **Objective:** Determine the probability that a randomly selected student is either male or has received an "A" grade. To solve this, we need to calculate: 1. Total students who are male. 2. Total students who received an "A". 3. Use the formula for probability with "or" condition: \[ P(\text{Male or A}) = P(\text{Male}) + P(\text{A}) - P(\text{Male and A}) \] - **Total students**: 63 - **Total males**: 35 - **Total students with an "A"**: 32 - **Males with an "A"**: 13 Using the formula: \[ P(\text{Male or A}) = \frac{35}{63} + \frac{32}{63} - \frac{13}{63} = \frac{54}{63} = \frac{18}{21} \approx 0.857 \] **Conclusion:** The probability that a randomly selected student is either male or received an "A" is approximately 0.857, or 85.7%.
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
![**Probability of Selecting a Male Student or a Student with an "A" Grade**
In this probability exercise, we analyze a group of students based on their grades and gender. The following table summarizes the distribution:
| | A | B | C | Total |
|--------|----|----|----|-------|
| Male | 13 | 8 | 14 | 35 |
| Female | 19 | 4 | 5 | 28 |
| Total | 32 | 12 | 19 | 63 |
**Objective:**
Determine the probability that a randomly selected student is either male or has received an "A" grade.
To solve this, we need to calculate:
1. Total students who are male.
2. Total students who received an "A".
3. Use the formula for probability with "or" condition:
\[
P(\text{Male or A}) = P(\text{Male}) + P(\text{A}) - P(\text{Male and A})
\]
- **Total students**: 63
- **Total males**: 35
- **Total students with an "A"**: 32
- **Males with an "A"**: 13
Using the formula:
\[
P(\text{Male or A}) = \frac{35}{63} + \frac{32}{63} - \frac{13}{63} = \frac{54}{63} = \frac{18}{21} \approx 0.857
\]
**Conclusion:**
The probability that a randomly selected student is either male or received an "A" is approximately 0.857, or 85.7%.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F71586c71-e002-40ed-a348-3617b1ab0846%2Fa98ea1a7-db71-4b69-bc35-88041acf397e%2Fxen1e6d.jpeg&w=3840&q=75)
Transcribed Image Text:**Probability of Selecting a Male Student or a Student with an "A" Grade**
In this probability exercise, we analyze a group of students based on their grades and gender. The following table summarizes the distribution:
| | A | B | C | Total |
|--------|----|----|----|-------|
| Male | 13 | 8 | 14 | 35 |
| Female | 19 | 4 | 5 | 28 |
| Total | 32 | 12 | 19 | 63 |
**Objective:**
Determine the probability that a randomly selected student is either male or has received an "A" grade.
To solve this, we need to calculate:
1. Total students who are male.
2. Total students who received an "A".
3. Use the formula for probability with "or" condition:
\[
P(\text{Male or A}) = P(\text{Male}) + P(\text{A}) - P(\text{Male and A})
\]
- **Total students**: 63
- **Total males**: 35
- **Total students with an "A"**: 32
- **Males with an "A"**: 13
Using the formula:
\[
P(\text{Male or A}) = \frac{35}{63} + \frac{32}{63} - \frac{13}{63} = \frac{54}{63} = \frac{18}{21} \approx 0.857
\]
**Conclusion:**
The probability that a randomly selected student is either male or received an "A" is approximately 0.857, or 85.7%.
Expert Solution
Step 1
Given information-
We have given the grades and gender of a group of students.
We have to find the probability that the student was male OR got an "A".
Step by step
Solved in 2 steps with 1 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
