Practice Proolems What is the maximuum vertical distance between the line u = x² 12x+45 cnd the paralbola y. for -3LX<15? %3D .2 y= Find F. f"(x)=-2+24x -12x², fl0)=2,f'(0)=16 %3D %3D

(a)
Consider the line and parabola
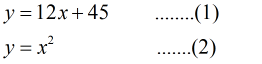
over [-3,15]
Let
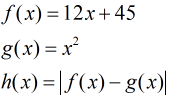
h(x) is the vertical distance between the points (x, f(x)) and (x,g(x)).
Actually we have maximize the h(x) over [-3,15] to find the maximum vertical distance,
And on the given interval [-3,15], f(x)≥g(x)
hence
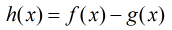
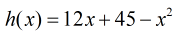
Critical points:
Critical points are the points where the derivative of the function either zero or does not exist.
Compute the derivative of h(x) and put it equal to zero
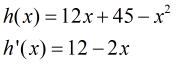
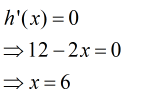
x=6 is the critical points of h(x)
Therefore, the candidates for the maximum of h(x) over the interval are x=6 (where h'(x)=0), and -3 and 15(end points of the interval)
Now evaluate the function value of h(x) at the critical point and end points
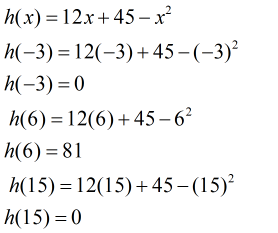
Clearly the h(x)=81 is the maximum value of h(x) over the interval [-3,15]
Hence the maximum vertical distance b/w the given line and parabola is 81.
Step by step
Solved in 5 steps with 18 images









