Homework Help is Here – Start Your Trial Now!
Math
Calculus
Power Series for Elementary Functions Function 1 = 1(x-1) + (x - 1)²(x - 1)³ + (x - 1)4+ (-1)" (x - 1)" +.. X 1 1 + x = 1- x + x²x³ + x4 x5 ++ (-1)"x" +... In x = (x- 1) et = 1 + x + sin x = x- cos x=1- arctan t = 1 arcsin x = x + p³ 3! 1.² 2! x3 3 r² 2! + + + (x - 1)² 2 x3 2.3 + ts 5! x4 4! ts 5 + x³ 3! - + + (x - 1)³ (x - 1)4 3 4 x4 4! x7 1⁹ + 7! 9! +6 x8 + 6! 8! x7 1⁹ + 7 9 1. 3x5 2 4 5 + + + rs 5! +.. + + ·· + + X" ++ +... (-1)" x2n+1 (2n + 1)! 1.3.5x7 2.4.6.7 (-1)" x2n (2n)! (-1)" x2n+1 2n + 1 +... +... (-1)"-¹(x-1)" n +... ++ (2n)!x2+1 (2"n!)2(2n + 1) + +... k(k-1)(k 2)x³ k(k-1)(k-2)(k - 3)x4 (1 + x) = 1 + kx + k(k-1)x² 2! + 3! 4! * The convergence at x = ±1 depends on the value of k. +... Interval of Convergence 0 < x < 2 -1

Power Series for Elementary Functions Function 1 = 1(x-1) + (x - 1)²(x - 1)³ + (x - 1)4+ (-1)" (x - 1)" +.. X 1 1 + x = 1- x + x²x³ + x4 x5 ++ (-1)"x" +... In x = (x- 1) et = 1 + x + sin x = x- cos x=1- arctan t = 1 arcsin x = x + p³ 3! 1.² 2! x3 3 r² 2! + + + (x - 1)² 2 x3 2.3 + ts 5! x4 4! ts 5 + x³ 3! - + + (x - 1)³ (x - 1)4 3 4 x4 4! x7 1⁹ + 7! 9! +6 x8 + 6! 8! x7 1⁹ + 7 9 1. 3x5 2 4 5 + + + rs 5! +.. + + ·· + + X" ++ +... (-1)" x2n+1 (2n + 1)! 1.3.5x7 2.4.6.7 (-1)" x2n (2n)! (-1)" x2n+1 2n + 1 +... +... (-1)"-¹(x-1)" n +... ++ (2n)!x2+1 (2"n!)2(2n + 1) + +... k(k-1)(k 2)x³ k(k-1)(k-2)(k - 3)x4 (1 + x) = 1 + kx + k(k-1)x² 2! + 3! 4! * The convergence at x = ±1 depends on the value of k. +... Interval of Convergence 0 < x < 2 -1

Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
See similar textbooks
icon
Related questions
Question

I need help with number 2. 

**Power Series for Elementary Functions** | **Function** | **Interval of Convergence** | |--------------------------------------------------------------|-----------------------------| | \(\frac{1}{x} = 1 - (x-1) + (x-1)^2 - (x-1)^3 + (x-1)^4 - \ldots + (-1)^n(x-1)^n + \ldots\) | \(0 < x < 2\) | | \( \frac{1}{1+x} = 1 - x + x^2 - x^3 + x^4 - x^5 + \ldots + (-1)^n x^n + \ldots \) | \(-1 < x < 1\) | | \(\ln x = (x-1) - \frac{(x-1)^2}{2} + \frac{(x-1)^3}{3} - \frac{(x-1)^4}{4} + \ldots + (-1)^{n-1}\frac{(x-1)^n}{n} + \ldots \) | \(0 < x \leq 2\) | | \(e^x = 1 + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots + \frac{x^n}{n!} + \ldots \) | \(-\infty < x < \infty\) | | \(\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} - \ldots + \frac{(-1)^n x^{2n+1}}{(2n+1)!} + \ldots\) | \(-\infty < x < \infty\) | | \(\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - \ldots + \frac{(-1)^n x^{2n}}{
Transcribed Image Text:**Power Series for Elementary Functions** | **Function** | **Interval of Convergence** | |--------------------------------------------------------------|-----------------------------| | \(\frac{1}{x} = 1 - (x-1) + (x-1)^2 - (x-1)^3 + (x-1)^4 - \ldots + (-1)^n(x-1)^n + \ldots\) | \(0 < x < 2\) | | \( \frac{1}{1+x} = 1 - x + x^2 - x^3 + x^4 - x^5 + \ldots + (-1)^n x^n + \ldots \) | \(-1 < x < 1\) | | \(\ln x = (x-1) - \frac{(x-1)^2}{2} + \frac{(x-1)^3}{3} - \frac{(x-1)^4}{4} + \ldots + (-1)^{n-1}\frac{(x-1)^n}{n} + \ldots \) | \(0 < x \leq 2\) | | \(e^x = 1 + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots + \frac{x^n}{n!} + \ldots \) | \(-\infty < x < \infty\) | | \(\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} - \ldots + \frac{(-1)^n x^{2n+1}}{(2n+1)!} + \ldots\) | \(-\infty < x < \infty\) | | \(\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - \ldots + \frac{(-1)^n x^{2n}}{
Expert Solution
Step 1

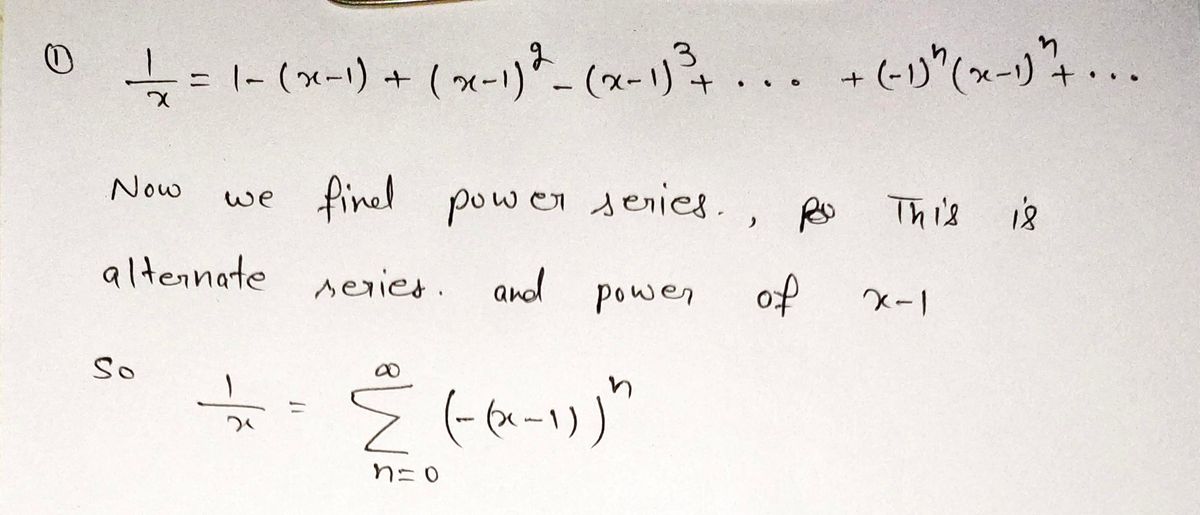
Calculus homework question answer, step 1, image 1

trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Precalculus
Precalculus
Calculus
ISBN:
9780135189405
Author:
Michael Sullivan
Publisher:
PEARSON
Calculus: Early Transcendental Functions
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS