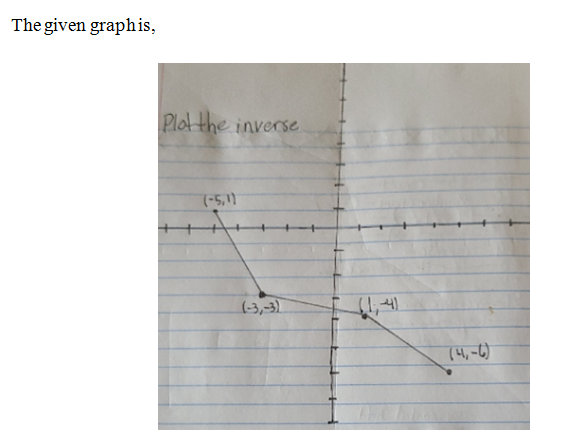
Plot the inverse 11'5-) (3,-3) (4,-6)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Concept explainers
Equations and Inequations
Equations and inequalities describe the relationship between two mathematical expressions.
Linear Functions
A linear function can just be a constant, or it can be the constant multiplied with the variable like x or y. If the variables are of the form, x2, x1/2 or y2 it is not linear. The exponent over the variables should always be 1.
Question
100%

Transcribed Image Text:**Title: Understanding Inverse Functions Through Graph Plotting**
**Overview:**
This image contains a handwritten graph that illustrates the concept of plotting the inverse of a function. The graph is drawn on lined paper using a Cartesian coordinate system, showcasing a series of plotted points connected by lines.
**Details of the Graph:**
- **Coordinate System:**
- The horizontal axis (x-axis) and the vertical axis (y-axis) intersect at the origin, marked by regular intervals.
- The axes are labeled with numerical values, but specific units are not denoted.
- **Plotted Points and Lines:**
- Four key points are marked and labeled with their coordinates:
- \((-5, 1)\)
- \((-3, -3)\)
- \((1, -4)\)
- \((4, -6)\)
- These points are connected with straight lines to form a piecewise linear graph.
- The lines create a visual representation of the plotted inverse function.
**Instruction:**
- The handwritten note next to the graph reads "Plot the inverse," indicating the focus is on understanding how to reverse the roles of dependent and independent variables in function plotting.
**Educational Objective:**
- This graphic aids in visualizing the relationship between functions and their inverses, helping students apply the concept by interpreting and plotting the inverse function on a graph.
Understanding how to interchange the x and y coordinates to form an inverse relationship is an essential skill in mathematics, reflecting symmetry over the line \(y = x\).
Expert Solution
Step 1
Step 2

Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

