Please help me solve this question and explain into detials. I am told we will have to draw a triangle but I dont know how. Can you help with this please? A point v = (x, y) is chosen uniformly at random from the triangular region with vertices at the points (0, 0), (2, 0), and (0, 2). Let A denote the event that x ≤ y. Let B denote the event that x ≤ 1. Let C denote the event that x + y ≤ 1. (a) Are A and B independent? Why, or why not? (b) Are A and C independent? Why, or why not?
Please help me solve this question and explain into detials. I am told we will have to draw a triangle but I dont know how. Can you help with this please? A point v = (x, y) is chosen uniformly at random from the triangular region with vertices at the points (0, 0), (2, 0), and (0, 2). Let A denote the event that x ≤ y. Let B denote the event that x ≤ 1. Let C denote the event that x + y ≤ 1. (a) Are A and B independent? Why, or why not? (b) Are A and C independent? Why, or why not?
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
Please help me solve this question and explain into detials. I am told we will have to draw a triangle but I dont know how. Can you help with this please?
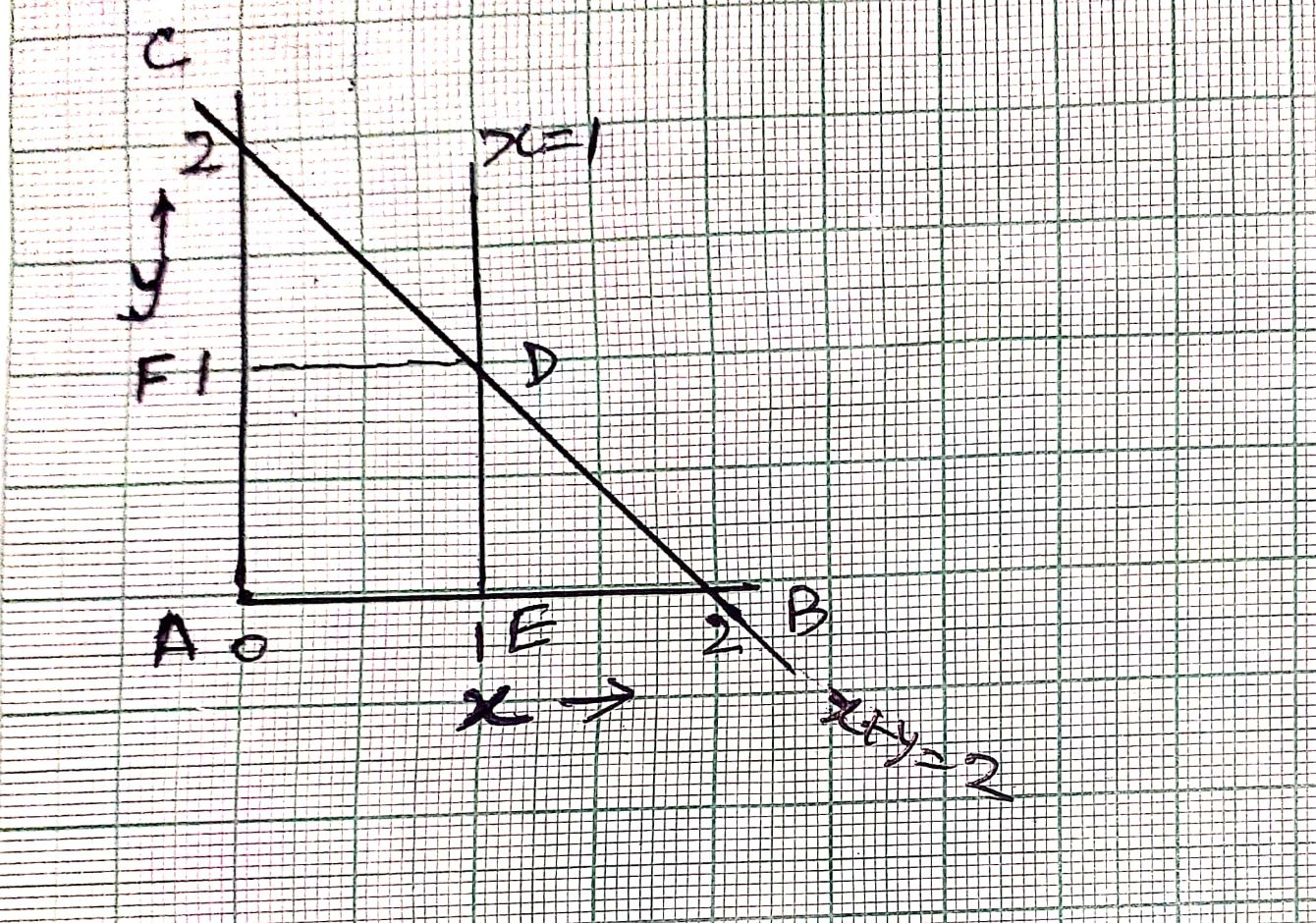
A point v = (x, y) is chosen uniformly at random from the triangular region with vertices at the points (0, 0), (2, 0),
and (0, 2).
Let A denote the
Let B denote the event that x ≤ 1.
Let C denote the event that x + y ≤ 1.
(a) Are A and B independent? Why, or why not? (b) Are A and C independent? Why, or why not?
Expert Solution
Step 1: Independence of Events shown.
The triangle is ABC whose area is
P(X) =
= 0.50 =P(A)

P(X1) =
=0.75 = P(B)
Step by step
Solved in 3 steps with 17 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
