
The problem is based on the Pascal’s Law of transmission of fluid pressure in an incompressible fluid.
The downward force F1 due to the car of mass m on the hydraulic platform is calculated as,
F1 = mg
Here g is the acceleration due to gravity.
Substitute 10000 kg for m, 9.8 m/s2 for g and solve for F1 as
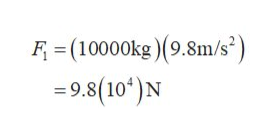
Pressure per unit area on the main cylinder of radius r due to the car is calculated as,
P1 = F1 / A1
The expression for area is computed as,
A1 = πr2
Substitute 10 cm for r and 3.14 for π and solve for A1. Further Substitute 9.8(104) N for F1 and the computed value of A1 in the expression for the pressure P1 exerted on the cylindrical platform and compute P1

Since the pressure has to be same on both the ends for the car to be raised on the hydraulic platform
The pressure P2 of the compressed air must be equal to the pressure exerted by the car.
Hence
P1 = P2
Since the air is used in the compressed form for the lift. The pressure P2 in the compressed cylinder will be,
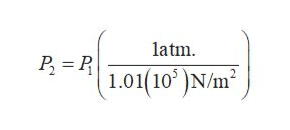
Step by step
Solved in 5 steps with 4 images









