Perform the Build Heap algorithm on the following array to output a Min heap. Draw the array following each downheap at the given index in the algorithm. Write your final answer in the Output row of the table. 0 null 1 70 2 20 3 10 4 45 5 30 6 15 7 5 8 25

Solution-
A binary tree that meets the heap property is referred to as a heap. There are two types of heaps:
The element at each node is greater than or equal to the element at its parent, according to the minimum heap. At the root is the element with the lowest value.
Max heap: Each node's element is smaller than the element at its parent. The root/parent element has the greatest value.
The term "heap" will always refer to min-heap via this image.
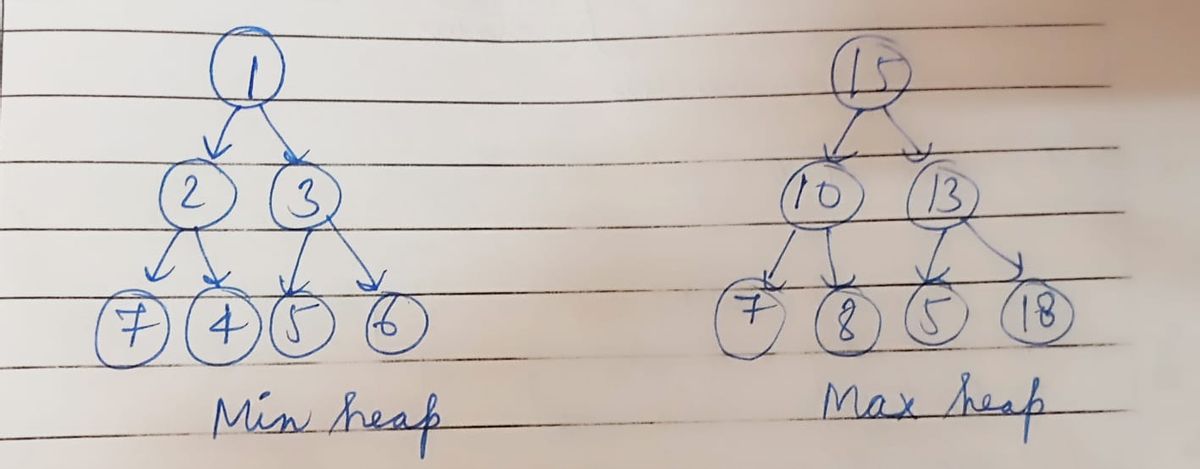
The lowest (or highest) priority element is always stored at the root of a heap, hence the name. Although it can be considered partially ordered, a heap is not a sorted structure. The aforementioned photos demonstrate that there is no clear hierarchy among the nodes at any level.
When you need to get rid of something of the lowest (or highest) priority, a heap comes in handy. Implementing a priority queue is one frequent usage of a heap.
Step by step
Solved in 4 steps with 6 images









