Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
I need help with this calc question

Transcribed Image Text:**Problem 8** is an algebra/limit problem which illustrates the power rule of derivatives being "derived" from the limit process. Most of you can see the answers without doing the algebra/limit process. I would like you to show the work that gives the answers without using the power rule. It is nice to give credit to those brilliant mathematicians (Newton and Leibniz) who developed calculus. The concept of limits has been around for over 2000 years but derivatives were developed in 1700.
9) Given \( f(x, y) = x^2 + y^2 \) use Algebra to find
a) \(\lim_{\Delta x \to 0} \frac{f(x + \Delta x, y) - f(x, y)}{\Delta x} \)
b) \(\lim_{\Delta y \to 0} \frac{f(x, y + \Delta y) - f(x, y)}{\Delta y} \)
Expert Solution
Step 1
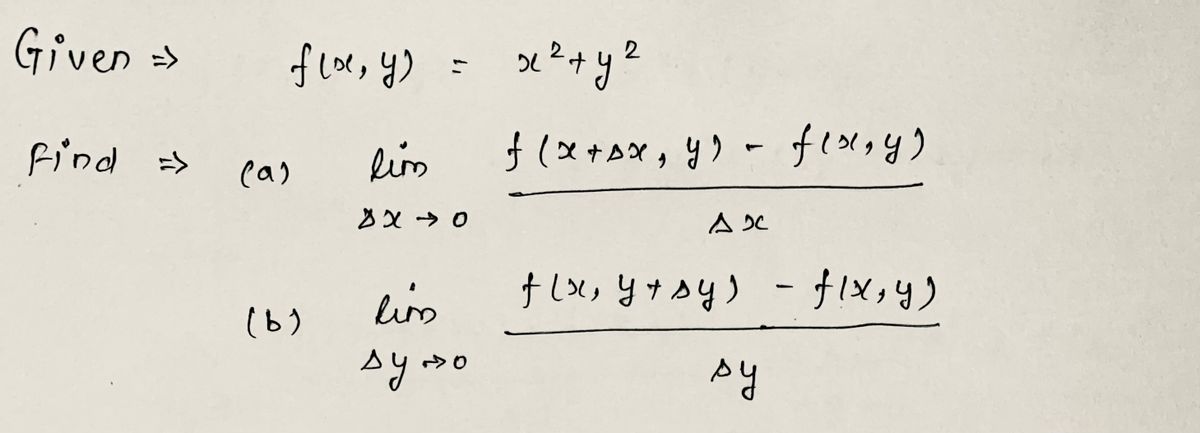
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning