Part E - Solving for Two Variables Now that you have one of the two variables in Part D isolated, use substitution to solve for the two variables. You may want to review the Multiplication and Division of Fractions and Simplifying a Expression Primers. Enter the answer as two numbers (either fraction or decimal), separated by a comma, with C first. ► View Available Hint(s) C, D= ΨΕΙ ΑΣΦ ?
Part E - Solving for Two Variables Now that you have one of the two variables in Part D isolated, use substitution to solve for the two variables. You may want to review the Multiplication and Division of Fractions and Simplifying a Expression Primers. Enter the answer as two numbers (either fraction or decimal), separated by a comma, with C first. ► View Available Hint(s) C, D= ΨΕΙ ΑΣΦ ?
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question

Transcribed Image Text:Part E - Solving for Two Variables
Now that you have one of the two variables in Part D isolated, use substitution to solve for the two variables. You may want to review the Multiplication and Division of Fractions and Simplifying an
Expression Primers.
Enter the answer as two numbers (either fraction or decimal), separated by a comma, with C first.
► View Available Hint(s)
C, D =
Submit
ΠΫΠΙ ΑΣΦ
?

Transcribed Image Text:Part D - Isolating a Variable with a Coefficient
In some cases, neither of the two equations in the system will contain a variable with a coefficient of 1, so we must take a further step to isolate it. Let's say we now have
3C + 4D = 5
2C+ 5D = 2
●
●
None of these terms has a coefficient of 1. Instead, we'll pick the variable with the smallest coefficient and isolate it. Move the term with the lowest coefficient so that it's alone on one side of its
equation, then divide by the coefficient. Which of the following expressions would result from that process?
D = ²/3 - ²/C
-³/C
C = 1-³/D
C=-D
3
○ D =
O
Submit
5
Previous Answers
Correct
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 10 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
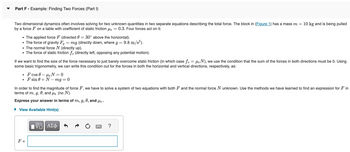
Transcribed Image Text:Part F - Example: Finding Two Forces (Part I)
Two dimensional dynamics often involves solving for two unknown quantities in two separate equations describing the total force. The block in (Figure 1) has a mass m = 10 kg and is being pulled
by a force F on a table with coefficient of static friction μs 0.3. Four forces act on it:
• The applied force F (directed 0 = 30° above the horizontal).
• The force of gravity Fg = mg (directly down, where 9 =
• The normal force N (directly up).
• The force of static friction f, (directly left, opposing any potential motion).
If we want to find the size of the force necessary to just barely overcome static friction (in which case ƒ = µN), we use the condition that the sum of the forces in both directions must be 0. Using
some basic trigonometry, we can write this condition out for the forces in both the horizontal and vertical directions, respectively, as:
F cos 0 μs N=0
F sin 0+N-mg = 0
F =
In order to find the magnitude of force F, we have to solve a system of two equations with both F and the normal force N unknown. Use the methods we have learned to find an expression for Fin
terms of m, g, 0, and μs (no N).
Express your answer in terms of m, g, 0, and μs.
View Available Hint(s)
= 9.8 m/s²).
ΠΫΠΙ ΑΣΦ
?
Solution
Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education