P(A) = 0.61, P(B) = 0.67, P(BU A) = 0.91 Find the following probabilities. P(AN B) = P(B|A) = P(A|B) =
Q: You are given the information that P(A) = 0.30 and P(B) = 0.40. (a) Do you have enough information…
A:
Q: Olivia is contemplating buying a laser printer. The probability that she will buy a printer…
A: Given data is : Probability that she she will buy a printer manufactured by Epson PE=0.21…
Q: Step 2 We are interested in the probabilities of finding r illiterate people, when r = 0, 1, 2, 3,…
A:
Q: Compute the following probabilities: If Y is distributed N (-4,4), Pr (Ys - 6) = .1587 . (Round your…
A:
Q: The probability of flu symptoms for a person not receiving any treatment is 0.03. In a clinical…
A: Define the random variable X follows Binomial distribution with n=1152 and p=0.03 Here, the sample…
Q: Given that P(A)P(A) = 0.4, P(B)P(B) = 0.51, and P(A∣B)P(A∣B) = 0.63, find the probabilities:…
A:
Q: Please solve the question attached
A: To find the expected profit, we need to use the expected value formula shown below.…
Q: Use the following probabilities to answer the question. Round to 4 decimal places.P(A) = 0.65, P (B)…
A: Given,
Q: 68% of U.S. adults have very little confidence in newspapers. You randomly select 10 U.S. adults.…
A: Given that Number of trials n=10 Probability of success p=0.68 X~bin(n,p)
Q: A recent survey by the New Statesman on British social attitudes asked respondents if they believe…
A: It is given that n = 6 and p = 0.63.
Q: In a computer instant messaging survey, respondents were asked to choose the most fun way to flirt,…
A: Option (a) is right.
Q: Given that P(A)P(A) = 0.49, P(B)P(B) = 0.63, and P(A∣B)P(A∣B) = 0.46, find the probabilities:…
A: As per our guidelines we can solve first three sub part of question and rest can be reposted.…
Q: Find the probability that the first traffic light is green given that the second traffic light is…
A: It is given that:P(A)=0.55;P(Ac)=0.45;P(B|A)=0.75P(B|Ac)=0.09;P(B)=0.453The objective is to find the…
Q: Given the probabilities shown below, what is P(A⋂B)? P(A) = 0.65 P(B) = 0.32 P(B|A) = 0.75
A: The provided information is:
Q: An animal shelter has a 65% adoption rate for puppies. Of all puppies in the shelter, 75% live to be…
A:
Q: Suppose P(A) = 0.2, P(B) - 0.45, and P(A n B) = 0.02. Find the following probabilities. P(A n B) =…
A: Given that, P(A) =0.2P(B) = 0.45P(A∩B)=0.02
Q: Tina plays college soccer. She makes a goal on 63 % of her attempts. On her next game she will…
A: From the provided information,
Q: Use the following probabilities to answer the question. Round to 4 decimal places. P(A)=0.19…
A:
Q: P(A)=0.64,P(B)=0.45,P(B∪A)=0.92 Find the following probabilities. P(A∩B) = P(B|A¯) = P(A¯|B) =
A: We have given that, P(A)=0.64, P(B)=0.45, P(B∪A) or P(AUB) =0.92 Then, We will find the following…
Q: In a computer instant messaging survey, respondents were asked to choose the most fun way to flirt,…
A:
Q: Use the following probabilities to answer the question. Round to 4 decimal places.…
A: The given probabilities are P(A)=0.66 , P(B)=0.29 and P(A and B)=0.05
Q: Use the following probabilities to answer the question. Round to 4 decimal places. P(A) = 0.75, P(B)…
A: Given: P(A) = 0.75, P(B) = 0.2, P(A and B) = 0.05.
Q: What would the expected value be if tickets were sold for $10 but there were 1000 tickets sold?…
A: To calculate the expected value (EV) for the raffle with the new parameters (tickets sold for $10…
Q: Use the following probabilities to answer the question. Round to 4 decimal places.…
A: Solution: Given information: P(A) =0.33 P(B)=0.62 P(A∩B)=0.05
Q: The probability of flu symptoms for a person not receiving any treatment is 0.024. In a clinical…
A: Given information: The probability of flu symptoms for a person not receiving any treatment is…
Q: According to a recent survey, the probability that the driver in a fatal vehicle accident is female…
A:
Q: Use the following probabilities to answer the question. Round to 4 decimal places P(A) 0.44, P(B)…
A: It is given thatThe conditional probability of B given A can be calculated as follows.
Q: Use the following probabilities to answer the question. Round to 4 decimal places. P(A) = 0.21, P(B)…
A: P(A) = 0.21 P(B) = 0.74 P(A and B) = 0.05 P(B|A) = ?
Q: 117.If A and B are independent events such that P(B) = P(AUB) = 0.8 then P(A) is
A:
Q: Suppose P(A) = 0.15, P(B) = 0.2, and P(A n B) = 0.06. Find the following probabilities. P(A n B) =…
A:

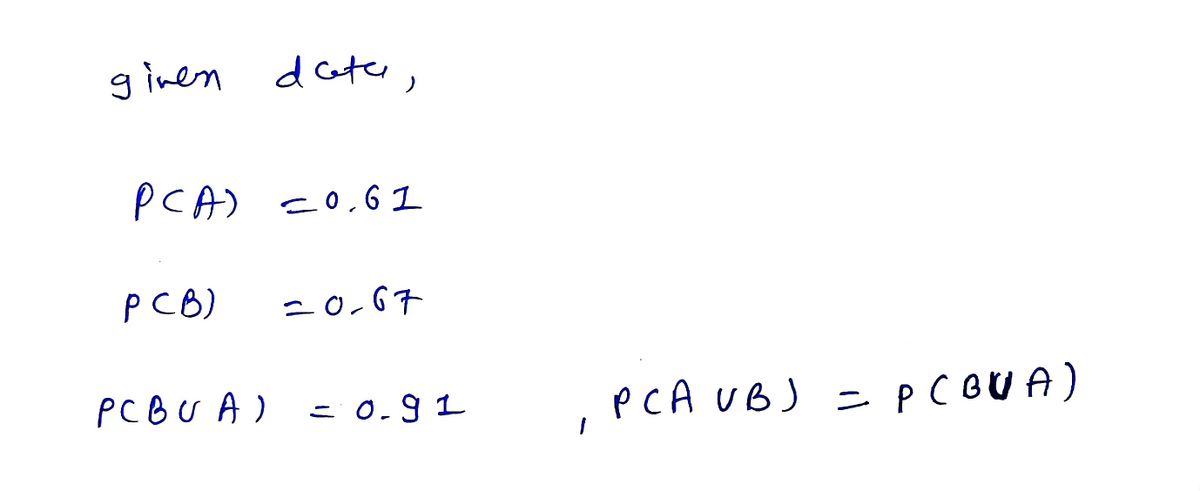
Step by step
Solved in 2 steps with 2 images

- According to a recent survey, the probability that the driver in a fatal vehicle accident is female (event F) is 0.2929. The probability that the driver is 24 years old or less (event A) is 0.1922. The probability that the driver is female and is 24 years old or less is 0.0529. Answer parts (a) through (d) below. (a) Find the probability of FUA. P(FUA) = (Round to four decimal places as needed.)A commuter must pass through 5 traffic lights on her way to work and will have to stop at each one that is red. She estimates the probability model for the number of red lights she hits, as shown in the table. Complete parts a and b. 03 11 X=# of red 1 2 P(X =x) 0.05 0.25 0.36 0.13 0.13 0.08 03 11 (a) How many red lights should she expect to hit each day? 11 Expect to hit red lights. (Round to one decimal place as needed.) 04 (b) What's the standard deviation? 11 04 (Round the final answer to one decimal place as needed. Round all intermediate values to three decimal places as needed.) 11 60nUse the following probabilities to answer the question. Round to 4 decimal places.P(A)=0.72P(A)=0.72, P(B)=0.18P(B)=0.18, P(AandB)=0.10P(AandB)=0.10.P(B∣A)=
- P (3)= 1/5 5. Mr. Henry has a basket full of fruit. He does not know how many pieces of fruit are in the basket. or the types of fruit. Each of the 20 students in his class selects one piece of fruit from the basket without looking, notes its fruit type, and then puts it back in the basket. Based on the results shown in the table, what can the students conclude about the probability of selecting an apple? Fruit Apple Orange Pear Number of 13 Pieces of Frruit Answer here: 6 The probability model based on experimental ETA 2.Given that P(A)P(A) = 0.37, P(B)P(B) = 0.36, and P(A∣B)P(A∣B) = 0.31, find the probabilities:P(B∣A)P(B∣A) = P(∼A)P(∼A) = P(∼B)P(∼B) = P(∼A∣B)P(∼A∣B) = P(∼B∣A)P(∼B∣A) = P(A∣∼B)P(A∣∼B) = P(B∣∼A)P(B∣∼A) =Use the following probabilities to answer the question. Round to 4 decimal places. P(A) = 0.61, P(B) = 0.29, P(A and B) = 0.10. P(B | A) =
- You are taking a college class and X represents the final grade you'll get. You believe you have the following probabilities of getting these grades. X P(X) A (4 points) .60 B (3 points) .30 C (2 points) .10 Find the mean of X assuming the grades are worth the given point values.Victoria plays college soccer. She makes a goal 70% of the time she shoots. Victoria is going to attempt two goals in a row in the next game. A = the event Victoria is successful on her first attempt. P(A) = 0.7. B = the event Victoria is successful on her second attempt. P(B) = 0.7. Victoria tends to shoot in streaks. The probability that she makes the second goal given that she made the first goal is 0.8.a. What is the probability that she makes both goals? b. What is the probability that Victoria makes either the first goal or the second goal?A burglar alarm system has six fail-safe components. The probability of each failing is 0.05. Find these probabilities. Express your answers up to 4 decimal places. a. Exactly three will fail. Answer: P(X=3) = b. Fewer than two will fail. Answer: P(X<2) = c. None will fail. Answer: P(X=0) =
- Car inspection: Of all the registered automobiles in Colorado, 5% fail the state emissions test. Fifteen automobiles are selected at random to undergo an emissions test. Round the answers to at least four decimal places. 8 Part: 0/4 Part 1 of 4 (a) Find the probability that exactly three of them fail the test. The probability that exactly three of them fail the test is X 5Solve the question pleaseMultiply probabilities? A traffic light at an intersection near Jamal's house is red 30 % of the time, green 10 % of the time, and yellow 60 % of the time. Jamal encounters this light in the morning on his way to work and again in the evening on his way home. Is the probability that the light is red both times equal to =×0.30.30.09 . Explain why or why not.



