P a | 01 ed- x→ n2 02 The two points are, respectively, at perpendicular distances a and b from the interface. The displacement from P to Q has the component d parallel to the interface, and we let x represent the coordinate of the point where the ray enters the second medium. Let t = 0 be the instant the light starts from P. (a) Show that the time at which the light arrives at Q is n, Va? x2 + n2 V b2 + (d – x)² + - t = + V2 (b) To obtain the value of x for which t has its minimum value, differentiate t with respect to x and set the derivative equal to zero. Show that the result implies n2(d – x) V b? + (d – x)² ' + (c) Show that this expression in turn gives Snell's law, n, sin(@,) = n, sin(@2).
In the figure below, a light ray travels from point P in medium 1 to point Q in medium 2. The two points are, respectively, at perpendicular distances a and b from the interface. The displacement from P to Q has the component d parallel to the interface, and we let x represent the coordinate of the point where the ray enters the second medium. Let t = 0 be the instant the light starts from P.
a) Show that the time at which the light arrives at Q is:
b) To obtain the value of x for which t has its minimum value, differentiate t with respect to x and set the derivative equal to zero. Show that the result implies
c)Show that this expression in turn gives Snell's law,

The ray diagram is given as shown
According to the ray diagram,
In right-angle triangle PAB,
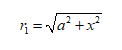
In right-angle triangle BDQ,
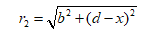
The time taken to travel from P to Q is the addition of time taken to travel from P to B and the time taken to travel B to Q.
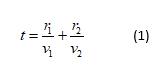
Here, v1 is the velocity in medium n1 and v2 is the velocity in medium n2.
The refractive index is given as,
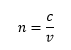
Substitute the n1 for n and v1 for v into the equation of the refractive index.
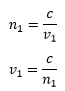
Substitute the n2 for n and v2 for v into the equation of the refractive index.
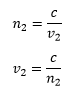
Substitute v1 and v2 into the expression (1).
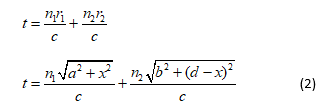
This is the time required to reach the light at Q.
Step by step
Solved in 4 steps with 13 images
