Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
Find the equation of the Tangent Line and Normal Line of the given equation at the given point. Graph the function a • f(x) = 2x²-3x² - 2x+5 Script 1% This program computes for the Tangent Line / Normal Line of a curve % about a given point %define x for symbolic processing 2 3 4 %IDENTIFY the function f(x) 5 f(x) = 2*x^3-3*x^2-2*x+5 7%DETERMINE the point of tangency (This will be a random point) 8 x0=randi ([-5,5]) 9 %SOLVE for the Ordinate of the point of tangency 10 y0=f(x0); %Evaluate y given value fo x 11 y= 2*x^3-3*x^2-2*x` 12 %FIND the slope function 13 yprime 6*(-5)^2-6*(-5)-2 14 15 %Determine the slope at the given xo 16 m 190 %Evaluate the slope 17 18 %Solve the equation of the tangent line 19 ytangent= 20 21 %Solve the Equation of the normal line 22 ynormal = 23 24 %DISPLAYING RESULTS 25 fprintf('The tangent line to f(x)=%s at (%.2f, %.2f) is y = %s\n', string (f(x)), x0, yo, string(ytam 26 fprintf('The normal line to f(x)=%s at (%.2f, %.2f) is y = %s \n', string(f(x)), x0, yo, string(ynorm 27 28 %PLOTTING 29 %Solve for the first derivative g1=ezplot(f.[-15.15]);

Find the equation of the Tangent Line and Normal Line of the given equation at the given point. Graph the function a • f(x) = 2x²-3x² - 2x+5 Script 1% This program computes for the Tangent Line / Normal Line of a curve % about a given point %define x for symbolic processing 2 3 4 %IDENTIFY the function f(x) 5 f(x) = 2*x^3-3*x^2-2*x+5 7%DETERMINE the point of tangency (This will be a random point) 8 x0=randi ([-5,5]) 9 %SOLVE for the Ordinate of the point of tangency 10 y0=f(x0); %Evaluate y given value fo x 11 y= 2*x^3-3*x^2-2*x` 12 %FIND the slope function 13 yprime 6*(-5)^2-6*(-5)-2 14 15 %Determine the slope at the given xo 16 m 190 %Evaluate the slope 17 18 %Solve the equation of the tangent line 19 ytangent= 20 21 %Solve the Equation of the normal line 22 ynormal = 23 24 %DISPLAYING RESULTS 25 fprintf('The tangent line to f(x)=%s at (%.2f, %.2f) is y = %s\n', string (f(x)), x0, yo, string(ytam 26 fprintf('The normal line to f(x)=%s at (%.2f, %.2f) is y = %s \n', string(f(x)), x0, yo, string(ynorm 27 28 %PLOTTING 29 %Solve for the first derivative g1=ezplot(f.[-15.15]);

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question

Can you please solve this using matlab codes. Thanks.

Find the equation of the Tangent Line and Normal Line of the given equation at the given point. Graph the function a ▪ f(x) = 2x³ - 3x2² - 2x+5 Script> 1 % This program computes for the Tangent Line / Normal Line of a curve % about a given point %define x for symbolic processing 2 3 4 %IDENTIFY the function f(x) 5 f(x) 2*x^3-3*x^2-2*x+5 6 7 %DETERMINE the point of tangency (This will be a random point) 8 x0=randi ([-5,5]) 9 %SOLVE for the Ordinate of the point of tangency 10 y0=f(x0); %Evaluate y given value fox 11 y= 2*x^3-3*x^2-2*x 12 %FIND the slope function 13 yprime = 6*(-5)^2-6*(-5)-2 14 15 %Determine the slope at the given xo 16 m= 190 %Evaluate the slope 17 18 %Solve the equation of the tangent line 19 ytangent= 20 21 %Solve the Equation of the normal line 22 ynormal = 23 D %Solve for the first derivative 28 %PLOTTING 29 g1-ezplot(f,[-15,151); 24 %DISPLAYING RESULTS 25 fprintf('The tangent line to f(x)=%s at (%.2f, %.2f) is y = %s\n', string (f(x)),x0,yo, string(ytar 26 fprintf('The normal line to f(x)=%s at (%.2f, %.2f) is y = %s \n',string(f(x)), x0, yo, string(ynorn 27
Transcribed Image Text:Find the equation of the Tangent Line and Normal Line of the given equation at the given point. Graph the function a ▪ f(x) = 2x³ - 3x2² - 2x+5 Script> 1 % This program computes for the Tangent Line / Normal Line of a curve % about a given point %define x for symbolic processing 2 3 4 %IDENTIFY the function f(x) 5 f(x) 2*x^3-3*x^2-2*x+5 6 7 %DETERMINE the point of tangency (This will be a random point) 8 x0=randi ([-5,5]) 9 %SOLVE for the Ordinate of the point of tangency 10 y0=f(x0); %Evaluate y given value fox 11 y= 2*x^3-3*x^2-2*x 12 %FIND the slope function 13 yprime = 6*(-5)^2-6*(-5)-2 14 15 %Determine the slope at the given xo 16 m= 190 %Evaluate the slope 17 18 %Solve the equation of the tangent line 19 ytangent= 20 21 %Solve the Equation of the normal line 22 ynormal = 23 D %Solve for the first derivative 28 %PLOTTING 29 g1-ezplot(f,[-15,151); 24 %DISPLAYING RESULTS 25 fprintf('The tangent line to f(x)=%s at (%.2f, %.2f) is y = %s\n', string (f(x)),x0,yo, string(ytar 26 fprintf('The normal line to f(x)=%s at (%.2f, %.2f) is y = %s \n',string(f(x)), x0, yo, string(ynorn 27
Expert Solution
steps

Step by step

Solved in 4 steps with 1 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

I would like to ask why the output of  y_theta is unrecognized.

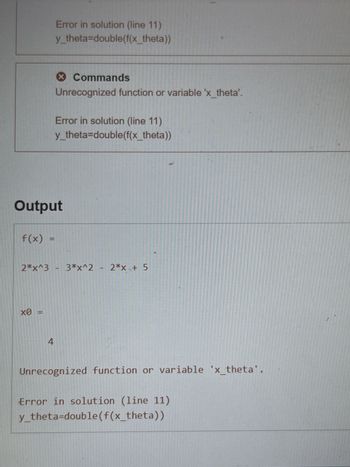
f(x) Error in solution (line 11) y_theta=double(f(x_theta)) Output х0 Commands Unrecognized function or variable 'x_theta'. 4 Error in solution (line 11) y_theta=double(f(x_theta)) 2*x^3 - 3*x^2 - 2*x + 5 Unrecognized function or variable 'x_theta Error in solution (line 11) y_theta=double(f(x_theta))
Transcribed Image Text:f(x) Error in solution (line 11) y_theta=double(f(x_theta)) Output х0 Commands Unrecognized function or variable 'x_theta'. 4 Error in solution (line 11) y_theta=double(f(x_theta)) 2*x^3 - 3*x^2 - 2*x + 5 Unrecognized function or variable 'x_theta Error in solution (line 11) y_theta=double(f(x_theta))
Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS