Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
pls find the derivitve
![The image presents two mathematical expressions that could be applied in different contexts such as calculus or algebra studies.
(c) \( y = \ln |x^3 - x^2| \)
This equation involves the natural logarithm of the absolute value of a polynomial expression. It's important to note the requirement of the absolute value to ensure the argument of the logarithm is non-negative, as logarithms are only defined for positive values.
(d) \( G(x) = \ln \left( \frac{a-x}{a+x} \right) \)
This function uses the natural logarithm of a rational expression. The presence of the logarithm indicates that the composition of \( (a-x) \) and \( (a+x) \) must remain positive for the function to be well-defined. This kind of expression might appear in calculus, particularly in integration or differentiation contexts.
(e) \( y = x^2 \ln[\ln x] \)
This equation combines both powers and nested logarithms. It implies that \( x \) must be greater than 1 for the inner natural logarithm to be defined (since \( \ln x > 0 \) is needed), highlighting a constraint on the domain. Such expressions are common in complex function analysis.
Each of these equations requires careful consideration of their domains and potential applications in mathematical problems.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F44d0f866-3879-4a95-bacc-717e14c65c8b%2Fd9d196d1-f714-49ea-9d59-26029a4069d5%2Fa840ogb_processed.png&w=3840&q=75)
Transcribed Image Text:The image presents two mathematical expressions that could be applied in different contexts such as calculus or algebra studies.
(c) \( y = \ln |x^3 - x^2| \)
This equation involves the natural logarithm of the absolute value of a polynomial expression. It's important to note the requirement of the absolute value to ensure the argument of the logarithm is non-negative, as logarithms are only defined for positive values.
(d) \( G(x) = \ln \left( \frac{a-x}{a+x} \right) \)
This function uses the natural logarithm of a rational expression. The presence of the logarithm indicates that the composition of \( (a-x) \) and \( (a+x) \) must remain positive for the function to be well-defined. This kind of expression might appear in calculus, particularly in integration or differentiation contexts.
(e) \( y = x^2 \ln[\ln x] \)
This equation combines both powers and nested logarithms. It implies that \( x \) must be greater than 1 for the inner natural logarithm to be defined (since \( \ln x > 0 \) is needed), highlighting a constraint on the domain. Such expressions are common in complex function analysis.
Each of these equations requires careful consideration of their domains and potential applications in mathematical problems.
Expert Solution
Step 1: Determine the given function
Since you have asked multiple questions in a single request so we will be answering only first question
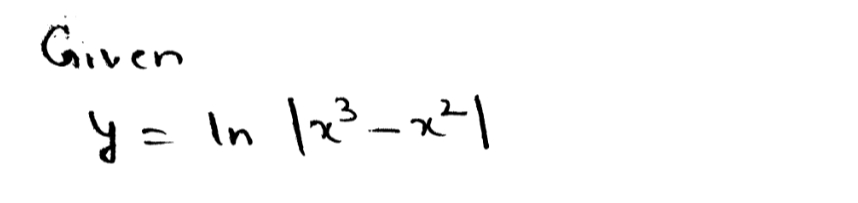
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning