Optional work many articles, the reduction of noise by resonant cavity is treated with the notion of acoustic impedance of the cavity, which is very low at resonant cavity. In this case the sound power at this frequency will be more directed toward the yavity in similar way electric current will be more directed to the branch of electric circuit where the resistance o In the is minimum. o Define the acoustic impedance in general case. o Express the acoustic impedance for quarter-wave resonator at open end and closed end. o Show that this impedance is almost zero for resonant frequency.

Acoustic impedance is the measurement of resistance that a system presents to the acoustic flow from an acoustic pressure be applied to the system.
In other words, it is the ratio of acoustic pressure (p) to acoustic volume flow (V). It is an intensive property of the medium.
A quarter-wave resonator is simply a pipe or tube closed at one end and open at the other. Hence the wall and rigid end of the tube confine a body of air within the resonator cavity. Under certain conditions, this body of air can be brought to a state of resonance.
Let us consider a tube of length L. the rigid end of the tube is located at x = 0 and open-end at x = L.
Let at the open end a source is continuously vibrating with frequency f. so when the source starts vibrating so the vibrations will move towards the rigid end and reflect off from rigid end and it will come to open end. So if we consider a piston at open end so there will be compression and rarefaction with the piston.
Now in order for the compression to arrive back at the open end after reflection, the source has moved through half a wavelength of its periodic motion and the compression has travelled two lengths of the resonator cavity. Hence
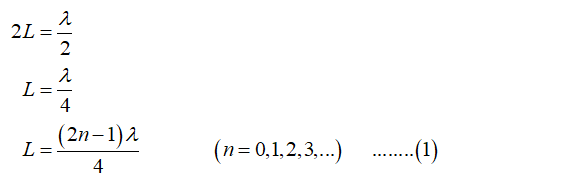
The wave equation is given as;
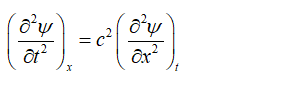
Now if ψ1 and ψ2 be the wave equation in one and other directions. The calculate for a resultant standing wave,
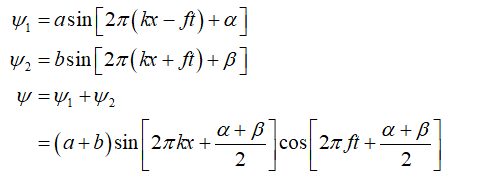
Step by step
Solved in 8 steps with 7 images
