ondiere Consider the diferential equation where O is a constant. iscifferential equation has an irreqular singular POint @ =D. Show that the substitution t yields the different ial equation d'y 2 dy + t dt + Ay=o which now has a reqularsinqular poit at t-o. dt2 b) Find two lincarly ihdependent Frobenius series sulutions 0f this new equation. C) Express each series solution af the original equatioh in terms of elementary functions 2. Consider tthe equat ion indicial equation has roots 4-420 ahose a) Derive the FrobeniuS scries solution n! (n-) 12u b) Substitute 2:Cy, nxt n in the equation xy"-y0 to derive e recurrence rtlation nni b= 2nt C. (nti)in! C) Conclude frorm uhis result that a seuond solution is n! (n-i! where H
Permutations and Combinations
If there are 5 dishes, they can be relished in any order at a time. In permutation, it should be in a particular order. In combination, the order does not matter. Take 3 letters a, b, and c. The possible ways of pairing any two letters are ab, bc, ac, ba, cb and ca. It is in a particular order. So, this can be called the permutation of a, b, and c. But if the order does not matter then ab is the same as ba. Similarly, bc is the same as cb and ac is the same as ca. Here the list has ab, bc, and ac alone. This can be called the combination of a, b, and c.
Counting Theory
The fundamental counting principle is a rule that is used to count the total number of possible outcomes in a given situation.
1. Parts a,b,& c

1 a,b,c) To solve the first differential equation by suitable coordinate transformation and power series technique
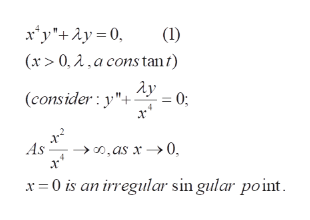
Solution to a)

b) First step in Frobenius method is to solve for the indices . here r =0 , -1. The difference is an integer. By the theory , Frobenius solution exists for r =0 (the larger root); Frobenius solution for r=-1 remains to be investigated.
Trending now
This is a popular solution!
Step by step
Solved in 6 steps with 6 images









